 por MateusDantas1 » Qui Fev 16, 2012 15:07
por MateusDantas1 » Qui Fev 16, 2012 15:07
Uma progressão aritmético-geométrica é uma sequência
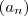
tal que
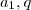
e

são números reais dados, com q diferente de 1 , e, para todo n inteiro, n > 0, tem-se que:

(A) Mostre por indução que
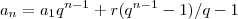
Eu ja provei a igualdade verdadeira para n=1:
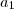
=
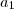


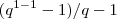
=>
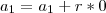
=>

verdade.
Suponhamos esta igualdade verdade para algum n. Para n + 1:

. Tentei resolver porém não consigo fazer a prova utilizando recorrência. Alguém pode me ajudar?
-
MateusDantas1
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qui Fev 16, 2012 14:51
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por fraol » Qui Fev 16, 2012 19:11
por fraol » Qui Fev 16, 2012 19:11
Use a hipótese de indução
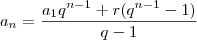
e a substitua na expressão dada
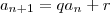
,
que ao desenvolver, você chegará no resultado desejado.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por RicardoSouza » Sex Fev 17, 2012 15:38
por RicardoSouza » Sex Fev 17, 2012 15:38
Peço, que por gentileza, alguém mostre ao menos mais um passo desta prova, pois já realizei vários cálculos e não obtive sucesso.
Grato,
-
RicardoSouza
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sex Fev 17, 2012 15:03
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por RicardoSouza » Sex Fev 17, 2012 15:38
por RicardoSouza » Sex Fev 17, 2012 15:38
Peço, que por gentileza, alguém mostre ao menos mais um passo desta prova por indução, pois já realizei vários cálculos e não obtive sucesso.
Grato,
-
RicardoSouza
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sex Fev 17, 2012 15:03
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por fraol » Sex Fev 17, 2012 16:04
por fraol » Sex Fev 17, 2012 16:04
Você chegou em

Foi dado que
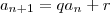
E a hipótese de indução é que
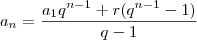
Então substituindo a hipótese na expressão
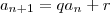
temos:
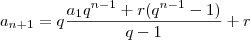
Agora desenvolvemos:
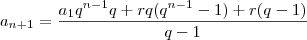
.
Você pode continuar. Ao terminar o desenvolvimento, você chegará à sua expressão o que prova a tese da indução.
Isso ajuda?
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por RicardoSouza » Sex Fev 17, 2012 16:45
por RicardoSouza » Sex Fev 17, 2012 16:45
Melhorou um pouco meus cálculos, mas ainda assim não cheguei à minha expressão.
Além do mais, achei que minha conta fosse igual à do Mateus, entretanto o

divide apenas o
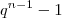
, que está após o r
De qualquer maneira, obrigado pela ajuda.
Editado pela última vez por
RicardoSouza em Sex Fev 17, 2012 17:25, em um total de 1 vez.
-
RicardoSouza
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sex Fev 17, 2012 15:03
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por fraol » Sex Fev 17, 2012 16:55
por fraol » Sex Fev 17, 2012 16:55
fraol escreveu:Agora desenvolvemos:
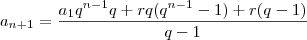
.
Continuando, os passos são:
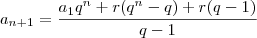
.

.

.
Dá uma olhadinha nessa última expressão, ela é a sua expressão.
Isso ajuda?
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por RicardoSouza » Sex Fev 17, 2012 17:05
por RicardoSouza » Sex Fev 17, 2012 17:05
Ajudou muito! Ainda estou decolando na indução(e na matemática), sempre cometo algum erro com as incógnitas...enfim..
Obrigado, vou revê-la e tentar resolver as próximas pelo método indutivo.
-
RicardoSouza
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sex Fev 17, 2012 15:03
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MateusDantas1 » Sex Fev 17, 2012 20:39
por MateusDantas1 » Sex Fev 17, 2012 20:39
ae galera, obrigado, agora eu entendi.
-
MateusDantas1
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qui Fev 16, 2012 14:51
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por RicardoSouza » Sex Fev 17, 2012 22:32
por RicardoSouza » Sex Fev 17, 2012 22:32
MateusDantas1 escreveu:ae galera, obrigado, agora eu entendi.
Mateus, você conseguiu o item (b)?
-
RicardoSouza
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sex Fev 17, 2012 15:03
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Victor Neumann » Qui Fev 23, 2012 21:57
por Victor Neumann » Qui Fev 23, 2012 21:57
Prezados Alunos,
Vocês deviam postar estas dúvidas no fórum do PIC2010, pois o seu moderador é o único autorizado a lhes dar as dicas que ele julgar necessárias.
Esta tarefa ficará aberta até o dia 11 de março de 2012, peço por favor que não continuem resolvendo este problema até esta data.
Agradeço pela atenção,
Victor Neumann
-
Victor Neumann
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Fev 23, 2012 21:37
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Prova por Indução (Soma de Progressão)
por RicardoSouza » Sex Fev 17, 2012 20:30
- 4 Respostas
- 4403 Exibições
- Última mensagem por nietzsche

Sex Mar 02, 2012 03:11
Progressões
-
- Uma prova por indução
por alexandre32100 » Ter Ago 17, 2010 01:11
- 2 Respostas
- 3258 Exibições
- Última mensagem por Guill

Qui Mai 03, 2012 00:01
Desafios Difíceis
-
- Prova por Indução
por Wania123 » Seg Jan 18, 2016 10:15
- 1 Respostas
- 4124 Exibições
- Última mensagem por adauto martins

Dom Jan 24, 2016 13:41
Cálculo: Limites, Derivadas e Integrais
-
- Questão prova concurso (progressão)
por fernandocez » Sáb Mar 12, 2011 23:32
- 2 Respostas
- 1792 Exibições
- Última mensagem por fernandocez

Qua Mar 16, 2011 00:19
Progressões
-
- [hipótese da indução] Indução matemática
por leonardoandra » Sáb Out 12, 2013 22:58
- 1 Respostas
- 2680 Exibições
- Última mensagem por leonardoandra

Seg Out 14, 2013 20:10
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
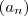 tal que
tal que 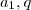 e
e  são números reais dados, com q diferente de 1 , e, para todo n inteiro, n > 0, tem-se que:
são números reais dados, com q diferente de 1 , e, para todo n inteiro, n > 0, tem-se que:
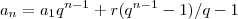
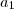 =
= 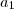


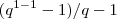
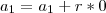 =>
=>  verdade.
verdade. . Tentei resolver porém não consigo fazer a prova utilizando recorrência. Alguém pode me ajudar?
. Tentei resolver porém não consigo fazer a prova utilizando recorrência. Alguém pode me ajudar?

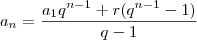
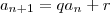 ,
,

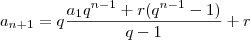
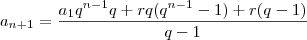 .
. divide apenas o
divide apenas o 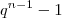 , que está após o r
, que está após o r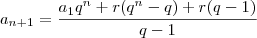 .
.  .
. .
. 




