 por lucas7 » Seg Jun 27, 2011 18:34
por lucas7 » Seg Jun 27, 2011 18:34
A sequência

;

;

é uma Progressão Aritmética crescente. O valor numérico da soma de seus termos é?
...para descobrir o x me aproveitei da fórmula a3 - a2 = a2 - a1, logo:
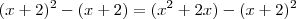
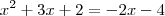
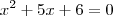
cheguei as raízes -2 e -3.
A resposta do gabarito é 3.
Alguém sabe onde errei?
Obrigado desde já.
ps: outra análise:
a1 + a2 = a3


subistuindo na soma dos termos todos valeriam 0.
O gênio, esse poder que deslumbra os olhos humanos, não é outra coisa senão a perseverança bem disfarçada.
Johann Goethe
-
lucas7
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Ter Fev 15, 2011 19:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Controle e Automação
- Andamento: cursando
 por Neperiano » Seg Jun 27, 2011 19:37
por Neperiano » Seg Jun 27, 2011 19:37
Ola
Olha a princípio o gabarito esta errado, fiz denovo aqui e confirmou a sua resposta, só se quando diz o valor númerico da sua soma ele quer que bote numeros positivos, qualquer coisa estarei tentando achar um erro.
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Soma de termos
por apotema2010 » Sex Fev 26, 2010 17:22
- 5 Respostas
- 6297 Exibições
- Última mensagem por Cleyson007

Dom Fev 28, 2010 08:50
Progressões
-
- Soma dos termos de uma PA
por 404040 » Dom Out 17, 2010 21:39
- 2 Respostas
- 3465 Exibições
- Última mensagem por 404040

Seg Out 18, 2010 17:55
Progressões
-
- [Soma n termos ] mostre que ....
por e8group » Qui Nov 08, 2012 19:08
- 3 Respostas
- 1933 Exibições
- Última mensagem por e8group

Qui Nov 08, 2012 20:32
Progressões
-
- [P.A] DETERMINAR A SOMA ODS 60 PRIMEIROS TERMOS
por ramonalado » Ter Mar 12, 2013 23:35
- 3 Respostas
- 12874 Exibições
- Última mensagem por Russman

Qua Mar 13, 2013 22:46
Progressões
-
- [retas perpendiculares] soma dos termos independentes
por JKS » Qua Ago 01, 2012 13:36
- 2 Respostas
- 3108 Exibições
- Última mensagem por JKS

Qua Ago 08, 2012 15:06
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 ;
;  ;
;  é uma Progressão Aritmética crescente. O valor numérico da soma de seus termos é?
é uma Progressão Aritmética crescente. O valor numérico da soma de seus termos é?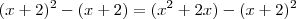
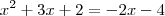
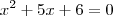







 , avisa que eu resolvo.
, avisa que eu resolvo.

