PA - Demonstração

[jessicaccs]

A questão é a seguinte:

Se numa PA a soma dos m primeiros termos é igual à soma dos n primeiros termos, 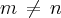, mostre que a soma m+n primeiros termos é igual a zero.


Considerei que m<n e desenvolvi . Consegui achar a seguinte relação: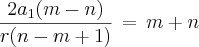

(I)

Em seguida desenvolvi

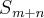
No final de tudo, joguei (I) nessa soma e achei:



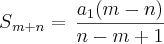
Não deu zero. Não sei se errei em alguma coisa durante a "sopa de letras" que fiz.

Depois tentei achar alguma outra relação.
Pensei o seguinte:
Se m<n, então, tenho que .
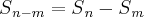Do enunciado eu posso tirar que:
E, portanto:

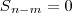
Logo:


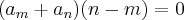
e,

Desenvolvendo-o, consegui achar a seguinte relação:

Mas, não consegui chegar a nenhum lugar com ela, também.

Obrigada.

[Elcioschin]

Como você não mostrou o desenvolvimento, não dá para saber onde você errou.
Veja a solução completa, considerando a1 = a como 1º termo

am = a + (m - 1)*r -----> Sm = (a + am)*m/2 ----> Sm = (2a + r*m - r)*m/2 ----> Sm = (2a*m + r*m² - r*m)/2

an = a + (n - 1)*r ------> Sn = (a + an)*n/2 ----> Sn = (2a + r*n - r)*n/2 ----> Sn = (2a*n + r*n² - r*n)/2

Igualando ----> (2a*m + r*m² - r*m)/2 = (2a*n + r*n² - r*n)/2 ----> r*m² - r*n² - r*m + r*n + 2a*m - 2a*n = 0

r*(m² - n²) - r*(m - n) + 2a*(m - n) = 0 ----> r*(m + n)*(m - n) - r*(m - n) + 2a*(m - n) = 0 ----> [r*(m + n - 1) - 2a]*(m - n) = 0

Como m <> n podemos dividir por m - n ----> r*(m + n - 1) + 2a = 0 ----> r*(m + n - 1) = - 2a ----> (I)


am+n = a + (m + n - 1)*r -----> Sm+n = [(2a + (m + n - 1)*r]/2 ----> (II)

Substituindo I em II ----> Sm+n = (2a - 2a)*r*n/2 -----> Sm+n = 0