 por DanielFerreira » Qua Jul 29, 2009 15:38
por DanielFerreira » Qua Jul 29, 2009 15:38
(UF-SE) Se os raios solares formam um ângulo ? com o solo, qual é, aproximadamente, o comprimento da sombra de um edifício com 10m de altura?
a) 16,6m
b) 15,5m
c) 14,4m
d) 13,3m
e) 12,2m
dado: sen a = 3/5
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Felipe Schucman » Qua Jul 29, 2009 19:01
por Felipe Schucman » Qua Jul 29, 2009 19:01
Desenhado a figura temos
Oposto a ?=10
Hipotenusa= H
Então sen ?=10/h=3/5--->h=16,66666
Lado da sombra= S
10 ^ 2 + S ^ 2 = 16,66666 ^ 2 ----> 13,33333333333333333333333333333 ---> aproximadamente....
Espero ter ajudado,
Um abraço!
-
Felipe Schucman
- Usuário Parceiro

-
- Mensagens: 52
- Registrado em: Ter Jul 28, 2009 17:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Economia e Direito
- Andamento: cursando
 por Cleyson007 » Qui Jul 30, 2009 11:55
por Cleyson007 » Qui Jul 30, 2009 11:55
Olá Danjr5!
Segue resolução ilustrada do problema:

O que está de frente para o ângulo é chamado de: Cateto oposto (logo: Co = 10m)
O que está em frente ao ângulo reto é chamado de hipotenusa (Note que você não tem o valor da hipotenusa).
Você quer encontrar o valor
x (cateto adjacente)
Sabe-se que:
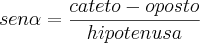
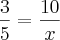
Multiplicando cruzado:
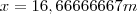
Espero ter ajudado!
Comente qualquer dúvida,

?
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Felipe Schucman » Qui Jul 30, 2009 14:15
por Felipe Schucman » Qui Jul 30, 2009 14:15
Bom dia Cleyson007,
Mas encontrei erros em sua resolução sen é cateto oposto/hipotenusa.....no caso o que você fez foi oposto/adjacente de forma que a relação da razão que você estabeleceu com a razão do seno é desse angulo dado é impossivel.
Se estiver errado me me diga! Espero ter ajudado!
Um abraço!
-
Felipe Schucman
- Usuário Parceiro

-
- Mensagens: 52
- Registrado em: Ter Jul 28, 2009 17:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Economia e Direito
- Andamento: cursando
 por Molina » Qui Jul 30, 2009 15:38
por Molina » Qui Jul 30, 2009 15:38
Boa tarde.
Como houve divergência no resultado, resolvi fazer também.
E cheguei em
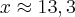
Abraços,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Cleyson007 » Qui Jul 30, 2009 17:22
por Cleyson007 » Qui Jul 30, 2009 17:22
Boa tarde Felipe, tudo bem?
Realmente... nem dá para acreditar que cometi um erro desses...
Vamos lá:
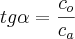
Pela
Relação Fundamental da Trigonometria, temos:
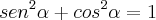
Estou encontrando:
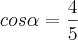
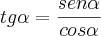
Logo,
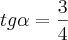
Resolvendo:
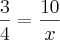
Portanto,
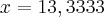
--> A resposta está igual a do Molina

Espero ter ajudado.
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Calculos envolvendo triângulo retângulo e retângulo
 por andersontricordiano » Seg Abr 18, 2011 02:29
por andersontricordiano » Seg Abr 18, 2011 02:29
- 1 Respostas
- 4030 Exibições
- Última mensagem por MarceloFantini

Seg Abr 18, 2011 04:19
Progressões
-
- Triangulo Retangulo
por ginrj » Qui Jun 04, 2009 18:56
- 1 Respostas
- 3406 Exibições
- Última mensagem por ginrj

Seg Jun 15, 2009 18:14
Geometria Plana
-
- Triângulo retangulo
por cristina » Seg Set 21, 2009 14:56
- 3 Respostas
- 2201 Exibições
- Última mensagem por DanielFerreira

Ter Set 22, 2009 14:18
Trigonometria
-
- Triângulo retângulo
por DanielFerreira » Qui Mar 03, 2011 11:26
- 1 Respostas
- 2118 Exibições
- Última mensagem por Elcioschin

Qui Mar 03, 2011 14:43
Geometria Plana
-
- Triângulo Retângulo
por nathyn » Qua Mar 21, 2012 16:35
- 1 Respostas
- 1600 Exibições
- Última mensagem por fraol

Dom Abr 08, 2012 00:12
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





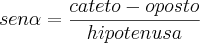
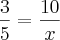
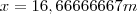
 ?
?

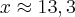


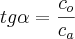
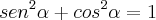
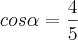
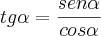
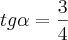
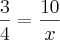
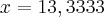




 , avisa que eu resolvo.
, avisa que eu resolvo.

