por nathyn » Qua Mar 21, 2012 16:35
por nathyn » Qua Mar 21, 2012 16:35
oiiee, tentei fazer essa questão mas nao consegui, se alguem poder me ajudar, por favor...
Seja o triângulo ABC, onde A(0, 0), B(2, 0) e C(2, 2?3). Se a medida do ângulo interno referente ao vértice A for reduzida em 50%, a área do triângulo ficará
a) 75% menor b) 50% menor c) 33% menor d) 30% menor e) 25% meno
Bom, eu montei o triangulo, usei teorema de pitagoras para encontrar a hipotenusa e usei a relação cosseno para achar os valores dos angulos e ficou assim:

Bom reduzindo em 50% o ângulo A sei que ficará:

Mas não sei qual a relação disso com os lados -(.
Me ajude por favor.
-
nathyn
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Qua Nov 16, 2011 14:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por fraol » Dom Abr 08, 2012 00:12
por fraol » Dom Abr 08, 2012 00:12
Seguindo os seus desenhos temos:
No primeiro triângulo, a área é:
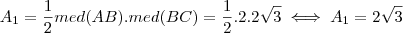
.
No segundo triângulo, a tangente de 30 graus é:
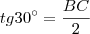
, mas
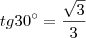
, então:
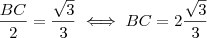
.
Assim, no segundo triângulo, a área é:

.
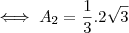
Observe que a área do segundo triângulo é igual a um terço da área do primeiro triângulo.
Então a área do segundo triângulo é dois terços menor do que a área do primeiro.
Como dois terços é igual a aproximadamente 67% então não há alternativa correta.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Calculos envolvendo triângulo retângulo e retângulo
 por andersontricordiano » Seg Abr 18, 2011 02:29
por andersontricordiano » Seg Abr 18, 2011 02:29
- 1 Respostas
- 4034 Exibições
- Última mensagem por MarceloFantini

Seg Abr 18, 2011 04:19
Progressões
-
- Triangulo Retangulo
por ginrj » Qui Jun 04, 2009 18:56
- 1 Respostas
- 3409 Exibições
- Última mensagem por ginrj

Seg Jun 15, 2009 18:14
Geometria Plana
-
- Triângulo retângulo
por DanielFerreira » Qua Jul 29, 2009 15:38
- 5 Respostas
- 6826 Exibições
- Última mensagem por Cleyson007

Qui Jul 30, 2009 17:22
Trigonometria
-
- Triângulo retangulo
por cristina » Seg Set 21, 2009 14:56
- 3 Respostas
- 2204 Exibições
- Última mensagem por DanielFerreira

Ter Set 22, 2009 14:18
Trigonometria
-
- Triângulo retângulo
por DanielFerreira » Qui Mar 03, 2011 11:26
- 1 Respostas
- 2123 Exibições
- Última mensagem por Elcioschin

Qui Mar 03, 2011 14:43
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




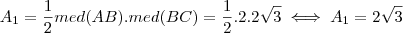 .
.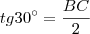 , mas
, mas 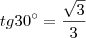 , então:
, então: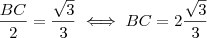 .
. .
.