 por Andreza » Qui Jan 19, 2012 11:36
por Andreza » Qui Jan 19, 2012 11:36
Um marceneiro precisa construir uma esquadria de madeira, conforme as informações:
AB=AC=60cm
BC=3,11cm
BE=3cm
BE perpendicular a AC
CD perpendicular a AB
Qual a medida de CD ?
Fazendo o desenho pude observar q os triangulos entre si sao isosceles, portanto a medidade CD seria igual a medida BC, ou seja, 3,11cm. ( Pelas relações entre congruência e semelhança de triângulos )
Não tenho o gabarito, por este motivo peço a ajuda de vcs para analisar se minha resposta está correta. Desde já estou muito grata.
-
Andreza
- Colaborador Voluntário

-
- Mensagens: 100
- Registrado em: Sáb Out 22, 2011 11:10
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Licenc. Plena Matemática
- Andamento: formado
 por fraol » Sex Jan 20, 2012 12:59
por fraol » Sex Jan 20, 2012 12:59
CD perpendicular a AB
Qual a medida de CD ?
Está faltando mais alguma informação em relação ao ponto D.
-
fraol
- Colaborador Voluntário

-
- Mensagens: 392
- Registrado em: Dom Dez 11, 2011 20:08
- Localização: Mogi das Cruzes-SP
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
 por ant_dii » Sáb Jan 21, 2012 03:35
por ant_dii » Sáb Jan 21, 2012 03:35
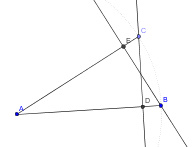
- um desenho possível
- esquadria2.png.jpg (5.91 KiB) Exibido 1807 vezes
Bom, esse foi um possível desenho, mas com as informações que deu...
eu encontrei como resposta para

, 3 e não 3,11...
Para isso observei que o ângulo
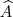
é comum aos triângulos

e
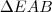
, e ambos possuem um ângulo reto, por isso são semelhantes...
daí que

...
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Descobrir a medida da sequência dos quadrados
 por MARCION » Seg Dez 15, 2014 15:34
por MARCION » Seg Dez 15, 2014 15:34
- 4 Respostas
- 4168 Exibições
- Última mensagem por MARCION

Ter Dez 16, 2014 08:05
Funções
-
- Criar fórmula simplificada para descobrir medida
por rodolfinho » Seg Jul 30, 2018 17:30
- 0 Respostas
- 2130 Exibições
- Última mensagem por rodolfinho

Seg Jul 30, 2018 17:30
Trigonometria
-
- Sistema de medida - medida de área
por Igra » Qui Abr 11, 2013 09:53
- 2 Respostas
- 4744 Exibições
- Última mensagem por Igra

Sex Abr 12, 2013 19:37
Conversão de Unidades
-
- [Descobrir taxa de taxa de juro] eliminar exp pra descobrir
por edgar1985 » Qua Ago 17, 2011 11:42
- 5 Respostas
- 3542 Exibições
- Última mensagem por Rogerio Murcila

Qui Ago 18, 2011 09:15
Matemática Financeira
-
- [Funções] Descobrir o f{f[f(x)]}
por Richard Oliveira » Qua Nov 30, 2011 12:37
- 3 Respostas
- 2626 Exibições
- Última mensagem por DanielFerreira

Dom Jan 08, 2012 16:31
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 , 3 e não 3,11...
, 3 e não 3,11...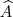 é comum aos triângulos
é comum aos triângulos  e
e 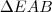 , e ambos possuem um ângulo reto, por isso são semelhantes...
, e ambos possuem um ângulo reto, por isso são semelhantes... ...
... em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.