por JoseEduardo » Dom Out 09, 2011 03:25
Caiu a seguinte questão na minha prova:
Seja ABC um triângulo retângulo cujos catetos medem 8 cm e 6 cm, respectivamente. Se D e um ponto sobre e o triângulo ADC e isósceles, a medida do segmento , em cm, é igual a:
a) 3/4 b) 15/6 c) 15/4 d) 25/4 e) 25/2
Dexei a questão em branco e estudando tentei resolvê-la:
Pelo pitágoras achei que hipotenusa AC = 10.E interpretei que AD = DC = X
Daí pra frente não sei como continuar.
-
JoseEduardo
- Novo Usuário
-
- Mensagens: 6
- Registrado em: Sex Set 10, 2010 01:45
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Estudante
- Andamento: cursando
por cpfdojr » Sáb Out 15, 2011 23:55
BOM, FIZ O SEGUINTE
COLOQUEI AD=AC=X TAMBEM, MAS SO QUE ASSIM FORMAMOS UM TRIANGULO RETANGULO ABD DE CATETOS AB=6, AD=X E BD=8-X. ASSIM, FAZEMOS PITAGORAS E SIMPLIFICANDO ACHAMOS X=
-
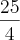
cpfdojr
- Novo Usuário
-
- Mensagens: 1
- Registrado em: Sáb Out 15, 2011 23:39
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
por JoseEduardo » Sex Nov 04, 2011 00:44
É isso mesmo, bate com o gabarito, valeu!
-
JoseEduardo
- Novo Usuário
-
- Mensagens: 6
- Registrado em: Sex Set 10, 2010 01:45
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Estudante
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Calculos envolvendo triângulo retângulo e retângulo
por andersontricordiano » Seg Abr 18, 2011 02:29
- 1 Respostas
- 3926 Exibições
- Última mensagem por MarceloFantini
Seg Abr 18, 2011 04:19
Progressões
-
- Triangulo Retangulo
por ginrj » Qui Jun 04, 2009 18:56
- 1 Respostas
- 3325 Exibições
- Última mensagem por ginrj
Seg Jun 15, 2009 18:14
Geometria Plana
-
- Triângulo retângulo
por DanielFerreira » Qua Jul 29, 2009 15:38
- 5 Respostas
- 6665 Exibições
- Última mensagem por Cleyson007
Qui Jul 30, 2009 17:22
Trigonometria
-
- Triângulo retangulo
por cristina » Seg Set 21, 2009 14:56
- 3 Respostas
- 2084 Exibições
- Última mensagem por DanielFerreira
Ter Set 22, 2009 14:18
Trigonometria
-
- Triângulo retângulo
por DanielFerreira » Qui Mar 03, 2011 11:26
- 1 Respostas
- 2029 Exibições
- Última mensagem por Elcioschin
Qui Mar 03, 2011 14:43
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Dom Jan 17, 2010 14:42
Não sei onde este tópico se encaixaria. Então me desculpem.
Eu não entendi essa passagem, alguém pode me explicar?
O livro explica da seguinte forma.
1°) P(1) é verdadeira, pois
2°) Admitamos que
, seja verdadeira:
(hipótese da indução)
e provemos que
Temos: (Nessa parte)
Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Seg Jan 18, 2010 01:55
Boa noite Fontelles.
Não sei se você está familiarizado com o
Princípio da Indução Finita, portanto vou tentar explicar aqui.
Ele dá uma equação, no caso:
E pergunta: ela vale para todo n? Como proceder: no primeiro passo, vemos se existe pelo menos um caso na qual ela é verdadeira:
Portanto, existe pelo menos um caso para o qual ela é verdadeira. Agora, supomos que
seja verdadeiro, e pretendemos provar que também é verdadeiro para
.
Daí pra frente, ele usou o primeiro membro para chegar em uma conclusão que validava a tese. Lembre-se: nunca saia da tese.
Espero ter ajudado.
Um abraço.
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Seg Jan 18, 2010 02:28
Mas, Fantini, ainda fiquei em dúvida na passagem que o autor fez (deixei uma msg entre o parêntese).
Obrigado pela ajuda, mesmo assim.
Abraço!
Assunto:
Princípio da Indução Finita
Autor:
Fontelles - Qui Jan 21, 2010 11:32
Galera, ajuda aí!
Por falar nisso, alguém conhece algum bom material sobre o assunto. O livro do Iezzi, Matemática Elementar vol. 1 não está tão bom.
Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Qui Jan 21, 2010 12:25
Boa tarde Fontelles!
Ainda não estou certo de qual é a sua dúvida, mas tentarei novamente.
O que temos que provar é isso:
, certo? O autor começou do primeiro membro:
Isso é verdadeiro, certo? Ele apenas aplicou a distributiva. Depois, partiu para uma desigualdade:
Que é outra verdade. Agora, com certeza:
Agora, como
é
a
, e este por sua vez é sempre
que
, logo:
Inclusive, nunca é igual, sempre maior.
Espero (dessa vez) ter ajudado.
Um abraço.
Assunto:
Princípio da Indução Finita
Autor:
Caeros - Dom Out 31, 2010 10:39
Por curiosidade estava estudando indução finita e ao analisar a questão realmente utilizar a desigualdade apresentada foi uma grande sacada para este problema, só queria tirar uma dúvida sobre a sigla (c.q.d), o que significa mesmo?
Assunto:
Princípio da Indução Finita
Autor:
andrefahl - Dom Out 31, 2010 11:37
c.q.d. = como queriamos demonstrar =)
Assunto:
Princípio da Indução Finita
Autor:
Abelardo - Qui Mai 05, 2011 17:33
Fontelles, um bom livro para quem ainda está ''pegando'' o assunto é:'' Manual de Indução Matemática - Luís Lopes''. É baratinho e encontras na net com facilidade. Procura também no site da OBM, vais encontrar com facilidade material sobre PIF... em alguns sites que preparam alunos para colégios militares em geral também tem excelentes materiais.
Assunto:
Princípio da Indução Finita
Autor:
MarceloFantini - Qui Mai 05, 2011 20:05
Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.
Assunto:
Princípio da Indução Finita
Autor:
Vennom - Qui Abr 26, 2012 23:04
MarceloFantini escreveu:Abelardo, faz 1 ano que o Fontelles não visita o site, da próxima vez verifique as datas.
Rpz, faz um ano que o fulano não visita o site, mas ler esse comentário dele enquanto respondia a outro tópico me ajudou. hAUEhUAEhUAEH obrigado, Marcelo. Sua explicação de indução finita me sanou uma dúvida sobre outra coisa.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
