 por ByRobert » Qui Set 01, 2011 12:59
por ByRobert » Qui Set 01, 2011 12:59
Boa tarde.
É possivel achar o valor de um angulo sabendo o seno,cosseno e tangente deste angulo? como ?
Após isso, Com o valor de um angulo e de um cateto, é possivel achar o valor de outro cateto? como?
obrigado.
-
ByRobert
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Set 01, 2011 12:45
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnologia da Informação
- Andamento: formado
 por Neperiano » Qui Set 01, 2011 15:16
por Neperiano » Qui Set 01, 2011 15:16
Ola
Claro que sim
Se você sabe que tang alfa = 50
Voce tenque calcular alfa, usando a inversa da tangente, representada por tang^-1
Nas calculadores cientificas tem
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por ByRobert » Qui Set 01, 2011 19:22
por ByRobert » Qui Set 01, 2011 19:22
Mas qual a formula pra resolver este problema na mão ?
-
ByRobert
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Set 01, 2011 12:45
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Tecnologia da Informação
- Andamento: formado
 por Neperiano » Qui Set 01, 2011 19:50
por Neperiano » Qui Set 01, 2011 19:50
Ola
Cara a mão pra tangente não sei faze, sei que pra inversa de seno, se usa 1/cos
Para tangente = seno/cosseno, então tang-1 que é cotangente é cosseno/seno, mas tente fazer e não deu, então usa uma calculadora que é mais fácil, xd
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por MarceloFantini » Qui Set 01, 2011 19:58
por MarceloFantini » Qui Set 01, 2011 19:58
A maneira de calcular um ângulo qualquer dado uma função trigonométrica dele é trabalhosa demais para ser feita na mão, inclusive não sei o método e acredito que seja um pouco complicado de se encontrar. O mais prático é sempre encontrar uma calculadora científica e usar a função inversa.
Neperiano, tome cuidado com o que você diz. A função
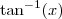
é diferente de
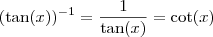
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Neperiano » Qui Set 01, 2011 20:04
por Neperiano » Qui Set 01, 2011 20:04
Ola
Ops, tem razão, tenho que aprender a escrever com latex, para não me complicar
Obrigado
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por LuizAquino » Qui Set 01, 2011 21:24
por LuizAquino » Qui Set 01, 2011 21:24
MarceloFantini escreveu:A maneira de calcular um ângulo qualquer dado uma função trigonométrica dele é trabalhosa demais para ser feita na mão, inclusive não sei o método e acredito que seja um pouco complicado de se encontrar.
O
Método de Newton pode ser usado para resolver esse problema.
Vejam a discussão no tópico:
Como calcular tangente a menos 1viewtopic.php?f=109&t=4390Apenas por curiosidade, muito antes da popularização das calculadoras, o seno, cosseno e tangente dos ângulos eram disponibilizados em tabelas, que eram obtidas através da aplicação de identidades trigonométricas e do conhecimento de alguns ângulos elementares, como por exemplo, 30°, 45° e 60°.
Se desejarem, leiam mais um pouco sobre isso em:
História da trigonometria.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Ângulos
 por admin » Sex Set 07, 2007 06:42
por admin » Sex Set 07, 2007 06:42
- 3 Respostas
- 13549 Exibições
- Última mensagem por Numwantida

Qui Mai 24, 2018 05:06
Pérolas
-
- ângulos
 por Thays » Sáb Jan 14, 2012 11:59
por Thays » Sáb Jan 14, 2012 11:59
- 6 Respostas
- 4604 Exibições
- Última mensagem por Thays

Qui Jan 19, 2012 09:36
Geometria Plana
-
- Angulos
 por silvia fillet » Sáb Fev 04, 2012 20:13
por silvia fillet » Sáb Fev 04, 2012 20:13
- 1 Respostas
- 2475 Exibições
- Última mensagem por Arkanus Darondra

Sáb Fev 04, 2012 22:06
Geometria Plana
-
- angulos
por alfabeta » Qui Mar 01, 2012 15:13
- 3 Respostas
- 2815 Exibições
- Última mensagem por timoteo

Sex Mar 02, 2012 01:00
Geometria Plana
-
- [ângulos]
 por Ederson_ederson » Qui Jul 02, 2015 08:49
por Ederson_ederson » Qui Jul 02, 2015 08:49
- 3 Respostas
- 3320 Exibições
- Última mensagem por Ederson_ederson

Seg Jul 06, 2015 17:18
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.






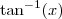 é diferente de
é diferente de 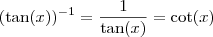 .
.



