Demonstração Relações Métricas

[PedroSantos]

Após alguma pesquisa encontrei uma forma de demonstrar algumas razões métricas de um triangulo retangulo.Nomeadamente:

-Cateto ao quadrado é igual ao produto da sua projecção sobre a hiputenusa pelo compromento da hipotenusa.


-O comprimento da altura relativa à hipotenusa ao quadrado é igual ao produto das projecções dos catetos sobre a hipotenusa.


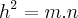
O método que encontrei, recorre à adição e ao produto escalar de vectores. Tomemos a seguinte figura:

triangulo1.png (3.01 KiB) Exibido 1758 vezes

Cada um dos vertices do triangulo têm uma identificação identica ao lado oposto e o pé da altura relativa à hipotenusa será denotado por H.

A primeira relação afirma que



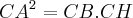
Então:



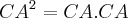
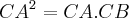( a projecção da hipotenusa sobre um eixo ortognal é o cateto-base)

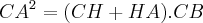(decomposição de CA nos seus elementos)

(os vectores HA e CB são prependiculares, o produto escalar é 0)



O vector CA corresponde ao cateto b, o CH corresponde à projecção de b sobre a hipotenusa e CB é o comprimento da hipotenusa.
Basta proceder de forma semelhante para a outra relação métrica.

Podem confirmar se o meu raciocino está correcto. Existem outras formas de demostrar estas relações métricas?

Fonte:
http://gilles.costantini.pagesperso-orange.fr/Lycee_fichiers/DevoirsP_fichiers/DM15.pdf

[VtinxD]

A forma que conheço para demonstra-las é através de semelhança entre os triângulos retângulos que aparecem na sua figura.