
Como o material de que são feitas as condutas não é susceptível de ser dobrado, o tubo tem de ser cortado em dois sítios. Qual o ângulo de corte
 ?
?Repara que, dividindo o tubo por um corte, segundo um ângulo
 , e rodando uma das partes 180º , é possível reajustar as secções.
, e rodando uma das partes 180º , é possível reajustar as secções. 
Este é o enunciado.
Eu comecei por determinar
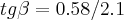 e determinei a amplitude do ângulo
e determinei a amplitude do ângulo  , mas depois não estou a perceber como hei de acabar o exercício.
, mas depois não estou a perceber como hei de acabar o exercício. PS: o resultado dá
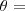 82,28º
82,28ºSe alguém me puder ajudar agradecia imenso.


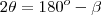

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)