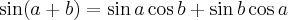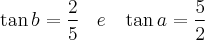por zenildo » Seg Mai 23, 2016 13:36
por zenildo » Seg Mai 23, 2016 13:36
Não consegui achar a resposta dessa questão. Tentei, porém consegui. Alguém, por favor me ajuda?
- Anexos
-

-
zenildo
- Colaborador Voluntário

-
- Mensagens: 309
- Registrado em: Sáb Abr 06, 2013 20:12
- Localização: SALVADOR-BA, TERRA DO AXÉ! BAÊA!!!!!
- Formação Escolar: EJA
- Área/Curso: PRETENDO/ DIREITO
- Andamento: cursando
 por zenildo » Ter Mai 24, 2016 11:00
por zenildo » Ter Mai 24, 2016 11:00
Estive analisando essa questão. Estou cônscio que o raciocínio seja o seguinte: a posição do raio na circunferência e o ângulo estabelecido nele determina se ele será cosseno ou seno. Além disso, percebemos que o valor do raio será igual em quaisquer posições da circunferência a medida que o comprimento do arco possui a mesma extensao do raio.Dessa forma,quando a questão diz:
4senA-10senB=0. Evidencia-se, pois uma relação de igualdade a partir destes dois membros: 4senA=10senB. Por outro lado, temos que saber deles serem de ângulos diferentes pela ocasião de haver: A e B. Avalia-se, a falta do cosseno para estabelecer as tangentes, logo estamos percebendo está numa Relação Fundamental!
Então fica:
4SenA=10senB
4CosB=10senB
4/10=senB/cosB
Tg= 2/5
4SenA=10SenB
4senA=10cosA
SenA/cosA= 10/4
SenA/cosA=5/2
-
zenildo
- Colaborador Voluntário

-
- Mensagens: 309
- Registrado em: Sáb Abr 06, 2013 20:12
- Localização: SALVADOR-BA, TERRA DO AXÉ! BAÊA!!!!!
- Formação Escolar: EJA
- Área/Curso: PRETENDO/ DIREITO
- Andamento: cursando
 por nakagumahissao » Qui Mai 26, 2016 02:34
por nakagumahissao » Qui Mai 26, 2016 02:34
Tem-se um sistema de equações:
![a + b = 90 \;\;\;\;[1] a + b = 90 \;\;\;\;[1]](/latexrender/pictures/a94dd4b3bb77180e3f46846f074f2ef1.png)
e
![4 \sin a - 10 \sin b = 0 \;\;\;\;[2] 4 \sin a - 10 \sin b = 0 \;\;\;\;[2]](/latexrender/pictures/74617189798fa333f0a2dd85fa03e5c1.png)
Trocando a em [2] por a = 90 - b e usando o seno das somas, você vai encontrar o tan b. Trocando b por b = 90 - a e usando o seno das somas, você acabará encontrando a tangente de a. Tente.
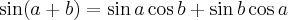
lembrando que cos(-x) = cos(x) e que sen(-x) = -sen(x)
As respostas sao
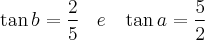
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
-
nakagumahissao
- Colaborador Voluntário

-
- Mensagens: 386
- Registrado em: Qua Abr 04, 2012 14:07
- Localização: Brazil
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Lic. Matemática
- Andamento: cursando
-
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- ajuda
por Daiane kelly » Seg Mar 24, 2008 22:38
- 4 Respostas
- 6377 Exibições
- Última mensagem por Cleyson007

Ter Mai 12, 2009 17:43
Matrizes e Determinantes
-
- Ajuda
por Umbus » Sáb Out 18, 2008 14:12
- 2 Respostas
- 3668 Exibições
- Última mensagem por lopes

Sáb Jun 20, 2009 15:51
Álgebra Linear
-
- Ajuda.
por VanessaFontela » Qui Dez 04, 2008 10:32
- 0 Respostas
- 2893 Exibições
- Última mensagem por VanessaFontela

Qui Dez 04, 2008 10:32
Matemática Financeira
-
- Ajuda!!!
por GABRIELA » Seg Set 21, 2009 17:28
- 1 Respostas
- 2283 Exibições
- Última mensagem por Molina

Seg Set 21, 2009 19:56
Sistemas de Equações
-
- Ajuda!!!!!!
por GABRIELA » Ter Set 22, 2009 16:35
- 6 Respostas
- 4412 Exibições
- Última mensagem por GABRIELA

Qui Set 24, 2009 16:29
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




![a + b = 90 \;\;\;\;[1] a + b = 90 \;\;\;\;[1]](/latexrender/pictures/a94dd4b3bb77180e3f46846f074f2ef1.png)
![4 \sin a - 10 \sin b = 0 \;\;\;\;[2] 4 \sin a - 10 \sin b = 0 \;\;\;\;[2]](/latexrender/pictures/74617189798fa333f0a2dd85fa03e5c1.png)