O exercício é da matéria de trigonometria...
De um ponto A, no solo, visam-se a base B e o Topo C de um bastão colocado verticalmente no alto de uma colina, sob ângulos de 30° e 45° respectivamente. Se o bastão mede 4m de comprimento, calcule a altura da colina, em metros.
fiz sobre a tg de 45° que seria co/ca mas o resultado dá quebrado tipo 5,46, tenho dificuldades no exercício.


 metros para a altura da colina que corresponde ao seu valor aproximado.
metros para a altura da colina que corresponde ao seu valor aproximado.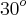 .
.

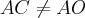 e
e 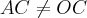 .
.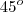 e não a tangente de
e não a tangente de 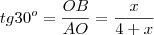

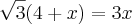
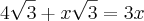
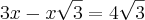


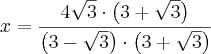
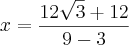

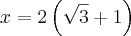 metros
metros
 .
.
 :
: