 por Cleyson007 » Sáb Mar 27, 2010 01:12
por Cleyson007 » Sáb Mar 27, 2010 01:12
Boa noite!

Gostaria de um esclarecimento sobre o procedimento que adotei para resolver o exercício acima.
No primero arco, calculei:


Minha dúvida está aqui: "Esse comprimento de 930m é o comprimento total do ângulo?" --> Acredito que seja, por isso, dividi o valor encontrado por 2, dado que o automóvel faz a curva.
No segundo arco, calculei:

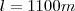
No terceiro arco, calculei:

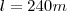
"Aqui também dividi o valor encontrado por 2, dado que o automóvel faz a curva."
Comprimento total: 3505m Está correto?
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Lucio Carvalho » Sáb Mar 27, 2010 18:34
por Lucio Carvalho » Sáb Mar 27, 2010 18:34
Olá Cleyson,
Li atentamente a tua resolução e não concordo com as divisões por "2" que decidiste fazer.
Basta multiplicar a amplitude em radianos de um ângulo ao centro numa circunferência e a medida do raio da circunferência para obter o comprimento do arco correspondente. Assim:
L1 = 600 m
L2 = 3,1 x 300 = 930 m
L3 = 600 m
L4 = 5,5 x 200 = 1100 m
L5 = 500 m
L6 = 2,4 x 200 = 480 m
Comprimento de uma volta na pista = 4210 m
-

Lucio Carvalho
- Colaborador Voluntário

-
- Mensagens: 127
- Registrado em: Qua Ago 19, 2009 11:33
- Localização: Rua 3 de Fevereiro - São Tomé
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Física/Química
- Andamento: formado
 por Cleyson007 » Dom Mar 28, 2010 11:02
por Cleyson007 » Dom Mar 28, 2010 11:02
Lucio Carvalho escreveu:Olá Cleyson,
Li atentamente a tua resolução e não concordo com as divisões por "2" que decidiste fazer.
Basta multiplicar a amplitude em radianos de um ângulo ao centro numa circunferência e a medida do raio da circunferência para obter o comprimento do arco correspondente. Assim:
L1 = 600 m
L2 = 3,1 x 300 = 930 m
L3 = 600 m
L4 = 5,5 x 200 = 1100 m
L5 = 500 m
L6 = 2,4 x 200 = 480 m
Comprimento de uma volta na pista = 4210 m
Bom dia Lucio!
Lucio, eu estava fazendo essa confusão devido pensar que automóvel percorre a metade dos arcos (devido ele não passar por dentro da pista).
Também estive analisando o exercício e percebi que os comprimento (l) que encontramos se refere ao comprimento formado pelo ângulo e não pelo comprimento total da circunferência.
Obrigado por esclarecer minha dúvida!
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- ARCOS
por MERLAYNE » Qua Abr 04, 2012 23:28
- 1 Respostas
- 1550 Exibições
- Última mensagem por MarceloFantini

Qua Abr 04, 2012 23:54
Trigonometria
-
- Arcos - ITA
por DanielFerreira » Dom Abr 29, 2012 21:13
- 1 Respostas
- 1577 Exibições
- Última mensagem por nakagumahissao

Dom Abr 29, 2012 23:28
Trigonometria
-
- Arcos e radianos
por Micheline » Qua Jan 28, 2009 10:13
- 7 Respostas
- 6848 Exibições
- Última mensagem por Sandra Piedade

Dom Fev 01, 2009 10:08
Trigonometria
-
- Trigonometria-Arcos
por rodsales » Sex Abr 17, 2009 21:27
- 2 Respostas
- 2209 Exibições
- Última mensagem por rodsales

Sáb Abr 18, 2009 16:57
Trigonometria
-
- Adição de Arcos
por Cleyson007 » Seg Mar 29, 2010 13:07
- 2 Respostas
- 3030 Exibições
- Última mensagem por Cleyson007

Ter Mar 30, 2010 11:43
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




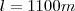

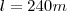 "Aqui também dividi o valor encontrado por 2, dado que o automóvel faz a curva."
"Aqui também dividi o valor encontrado por 2, dado que o automóvel faz a curva."

