 por Douglas13 » Qua Dez 02, 2015 09:40
por Douglas13 » Qua Dez 02, 2015 09:40
Como resolver essa questão. A receita marginal de uma empresa segue o modelo
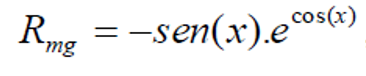
- Imagem2.png (14.09 KiB) Exibido 2958 vezes
então a expressão da receita total é dada por:
-
Douglas13
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qua Nov 25, 2015 10:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Economia
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [receita/custo marginal] Problema
por Revelants » Dom Out 05, 2008 14:32
- 1 Respostas
- 5104 Exibições
- Última mensagem por admin

Ter Out 14, 2008 14:58
Matemática Financeira
-
- funçoes marginal
por Sabrina » Sáb Mai 09, 2009 19:16
- 2 Respostas
- 1792 Exibições
- Última mensagem por Sabrina

Seg Mai 11, 2009 15:36
Funções
-
- [custo marginal] Problema
por Revelants » Dom Out 05, 2008 14:56
- 1 Respostas
- 3301 Exibições
- Última mensagem por admin

Ter Out 14, 2008 15:04
Matemática Financeira
-
- [Demanda e receita]
por camiscamila » Qui Mar 29, 2012 02:06
- 1 Respostas
- 6652 Exibições
- Última mensagem por LuizAquino

Qui Mar 29, 2012 13:04
Cálculo: Limites, Derivadas e Integrais
-
- Achar Receita Máxima
por Kathleen » Dom Jun 26, 2011 19:39
- 3 Respostas
- 3805 Exibições
- Última mensagem por Kathleen

Dom Jun 26, 2011 21:35
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.