Estou a precisar de ajuda pois não consigo resolver o seguinte exercício:
"Sabendo que tg ( pi + a ) = -?15 (menos raiz de quinze), e que "a" pertence ]
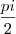 , pi [
, pi [Calcule o valor da expressão: cos(-a) + cos (
 pi + a) + tg a
pi + a) + tg aAgradecia que me explicassem o porquê de tg (pi +a) dar uma raíz negativa, uma vez que eu achei que tínhamos de reduzir tudo ao 1º quadrante, logo a tangente seria positiva...Não sei se perceberam a minha dúvida, mas qualquer coisa que não percebam digam nas respostas.


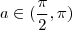 , então
, então  , isto é ,
, isto é , 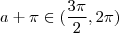 .
. 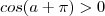 e
e 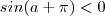 , segue que o quociente
, segue que o quociente  é sempre negativo . Por isso que o número
é sempre negativo . Por isso que o número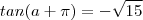 dado é negativo . Certo ?
dado é negativo . Certo ?![cos(-a) = cos(-a + [-\pi + \pi] ) = cos(-[a+\pi]+ \pi) = cos(-[a+\pi])cos(\pi) - sin(-[a+\pi])sin(\pi) = - cos(a+\pi) cos(-a) = cos(-a + [-\pi + \pi] ) = cos(-[a+\pi]+ \pi) = cos(-[a+\pi])cos(\pi) - sin(-[a+\pi])sin(\pi) = - cos(a+\pi)](/latexrender/pictures/1562f089af0bdb3e84d842a6ace653e3.png)
![cos(5/2 \pi + a ) = cos( \frac{3\pi}{2} + [\pi +a]) = cos(\frac{3\pi}{2})cos(\pi+a) - sin(\frac{3\pi}{2})sin(\pi +a) = cos(\pi +a) cos(5/2 \pi + a ) = cos( \frac{3\pi}{2} + [\pi +a]) = cos(\frac{3\pi}{2})cos(\pi+a) - sin(\frac{3\pi}{2})sin(\pi +a) = cos(\pi +a)](/latexrender/pictures/2cdff3bd07f457189e0f9c0a681fd800.png) .
. 
 pertencendo ao primeiro ,segundo ,terceiro ou quarto quadrante ,podemos reduzir o mesmo em relação ao primeiro quadrante.
pertencendo ao primeiro ,segundo ,terceiro ou quarto quadrante ,podemos reduzir o mesmo em relação ao primeiro quadrante. pertence ao quarto quadrante ,como vimos no post acima . O arco
pertence ao quarto quadrante ,como vimos no post acima . O arco  pertence
pertence  ,isto é , ele está no segundo quadrante .Sendo assim seria desnecessário reduzir a+\pi ao 1° quadrante .
,isto é , ele está no segundo quadrante .Sendo assim seria desnecessário reduzir a+\pi ao 1° quadrante . 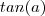 .Qual a relação entre
.Qual a relação entre 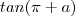 ?
? . A função tangente é periódica de período
. A função tangente é periódica de período  , logo para quaisquer que seja
, logo para quaisquer que seja  (com k inteiro ) teremos a igualdade
(com k inteiro ) teremos a igualdade 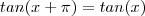 .Pode-se confirma esta igualdade utilizando a fórmula de adição de arcos .
.Pode-se confirma esta igualdade utilizando a fórmula de adição de arcos .![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)