 por mthc10 » Sáb Out 05, 2013 00:15
por mthc10 » Sáb Out 05, 2013 00:15
Olá amigos, estava resolvendo um problema e no final me deparei com a seguinte expressão:
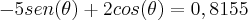
Preciso encontrar o valor de Theta(obvio hahaha). Não tive nenhuma ideia e nem lembro de alguma identidade trigonométrica que resolva tal equação, se alguém puder ajudar na solução ficarei grato!
-
mthc10
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Ter Mai 21, 2013 23:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharel em Engenharia Elétrica
- Andamento: cursando
 por Bravim » Sáb Out 05, 2013 15:19
por Bravim » Sáb Out 05, 2013 15:19
~.~
Editado pela última vez por
Bravim em Dom Out 06, 2013 02:36, em um total de 4 vezes.
-

Bravim
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Qui Out 03, 2013 03:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por mthc10 » Dom Out 06, 2013 01:09
por mthc10 » Dom Out 06, 2013 01:09
Amigo, o intervalo é de 0º à 360º.
Sendo assim, utilizando a fórmula que você deixou para eu calcular no intervalo de 0 até 2pi eu obtenho como resposta 20.37º. Porém, quando substituo este valor na equação original ela não satisfaz a igualdade...
Eu sei que a resposta que satisfaz a equação para o intervalo citado é 13,09º. Só não consigo chegar precisamente a este valor...
-
mthc10
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Ter Mai 21, 2013 23:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharel em Engenharia Elétrica
- Andamento: cursando
 por mthc10 » Dom Out 06, 2013 22:40
por mthc10 » Dom Out 06, 2013 22:40
Valeu irmão! Eu tava achando 13,7 pela aproximação que a calculadora faz, mas quando tu chamou de a o valor pequeno, não deu mais problemas!
Valeu mesmo!
-
mthc10
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Ter Mai 21, 2013 23:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharel em Engenharia Elétrica
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação - Como resolver problema com equação
por macedo1967 » Seg Set 25, 2017 10:13
- 3 Respostas
- 8702 Exibições
- Última mensagem por DanielFerreira

Dom Out 08, 2017 20:10
Equações
-
- Resolver a equação
por thadeu » Dom Nov 22, 2009 23:01
- 0 Respostas
- 834 Exibições
- Última mensagem por thadeu

Dom Nov 22, 2009 23:01
Álgebra Elementar
-
- Resolver equação
por anamendes » Sáb Jun 09, 2012 19:04
- 2 Respostas
- 1482 Exibições
- Última mensagem por DanielFerreira

Sáb Jun 09, 2012 19:20
Números Complexos
-
- [Ajuda] RESOLVER Equação
por hudsontr » Seg Out 10, 2011 17:44
- 1 Respostas
- 4372 Exibições
- Última mensagem por Neperiano

Ter Out 11, 2011 15:19
Trigonometria
-
- Equação polinomial (resolver em c)
por simonecig » Dom Set 26, 2021 21:42
- 2 Respostas
- 11394 Exibições
- Última mensagem por adauto martins

Qui Set 30, 2021 11:23
Polinômios
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
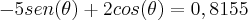

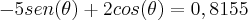




 para evitar de me confundir.
para evitar de me confundir.



![sin(x)=\frac{-10a\pm\sqrt[]{464-16a^2}}{58} sin(x)=\frac{-10a\pm\sqrt[]{464-16a^2}}{58}](/latexrender/pictures/93d699287ba9c0a5a3187e11eb419dbd.png)
![sin(x)=\frac{-5a\pm 2*\sqrt[]{29-a^2}}{29} sin(x)=\frac{-5a\pm 2*\sqrt[]{29-a^2}}{29}](/latexrender/pictures/4d6ffead280840687c6c254f0dab7578.png)
![x=arcsin(\frac{-5a\pm 2*\sqrt[]{29-a^2}}{29}) x=arcsin(\frac{-5a\pm 2*\sqrt[]{29-a^2}}{29})](/latexrender/pictures/d41a8eafbc9c1b25fecb4f0159bc95ed.png)


