As perguntas estão no anexo... Eu não conseguir fazer, pois sabendo da primeira resposta, dar para encontrar as outras... eu fiz desse jeito
0-0)
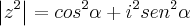, então irá dar: 
, pois 
.... Mas como vi no gabarito ele mostra que irá dar uma adição e não subtração, e estou com duvida nisso... Ah a também não entendi em relação aos afixos... Como vi a última (4-4), queria saber o motivo que não se eleva ao quadrado o i, pois essa (4-4) está verdadeira, e na justificativa mostra que i não foi elevado
por ![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)