 por gustavowelp » Qui Ago 16, 2012 00:49
por gustavowelp » Qui Ago 16, 2012 00:49
Olá! Boa noite!
Não sei como resolver esta questão. Se alguém puder me ajudar ficarei muito grato.
Qual a área, em km2, de um terreno triangular de vértices ABC sabendo que os ângulos ABC e CAB medem igualmente 35º e que a soma dos dois lados menores mede
20 km? Considere 0,94 como sendo o seno de 70º.
A resposta é 47
Muito obrigado
-
gustavowelp
- Usuário Parceiro

-
- Mensagens: 91
- Registrado em: Sex Jun 25, 2010 20:40
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: formado
 por Cleyson007 » Qui Ago 16, 2012 11:03
por Cleyson007 » Qui Ago 16, 2012 11:03
Bom dia Gustavo!
Temos que b + c = 20 Pelo fato dos ângulos serem iguais ----> b = c = 10
ângulo BÂC = 180º - 35º - 35º = 110º
S = b*c*sen110º/2 --->sen110º = sen(180º - 110º) = sen70º
S = 10*10*sen70º/2
S = 100*0,94/2
S = 47 km²
Espero ter ajudado.
Comente qualquer dúvida

-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por gustavowelp » Sex Ago 17, 2012 10:39
por gustavowelp » Sex Ago 17, 2012 10:39
Olá Cleyson!
Não entendi isto: sen110º = sen(180º - 110º) = sen70º
Também não entendi a fórmula da área: é lado * lado * sen(xº) / 2 ? Isto ?
Obrigado!!!
-
gustavowelp
- Usuário Parceiro

-
- Mensagens: 91
- Registrado em: Sex Jun 25, 2010 20:40
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: formado
 por Cleyson007 » Sex Ago 17, 2012 17:16
por Cleyson007 » Sex Ago 17, 2012 17:16
Boa tarde Gustavo!
Em resposta às suas dúvidas:
1ª) Tente entender pela imagem que fiz! (Em anexo)
2ª) A área de um triângulo pode ser obtida sabendo-se os lados dele. Sendo a e b dois lados quaisquer de um triângulo, e "alfa" o ângulo entre eles, temos que a área é:
A
t = a . b . sen (alfa) / 2 (Fonte:
http://pt.wikipedia.org/wiki/Tri%C3%A2ngulo )
Comente qualquer dúvida.
Abraço,
Cleyson007
- Anexos
-
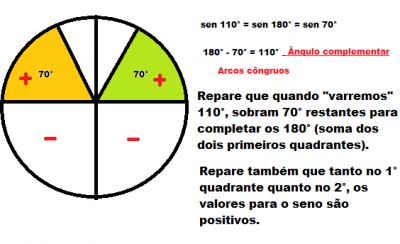
- Círculo Trigonométrico
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por gustavowelp » Sáb Ago 18, 2012 09:35
por gustavowelp » Sáb Ago 18, 2012 09:35
Muito obrigado Cleyson!!!!!
-
gustavowelp
- Usuário Parceiro

-
- Mensagens: 91
- Registrado em: Sex Jun 25, 2010 20:40
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Razão da área do triângulo para a área do quadrilátero]
 por Mayra Luna » Sex Nov 23, 2012 20:17
por Mayra Luna » Sex Nov 23, 2012 20:17
- 2 Respostas
- 4412 Exibições
- Última mensagem por Mayra Luna

Ter Nov 27, 2012 14:53
Geometria Plana
-
- [Área] Área de triangulo e trapézio
 por smlspirit » Qui Jul 19, 2012 20:07
por smlspirit » Qui Jul 19, 2012 20:07
- 1 Respostas
- 2996 Exibições
- Última mensagem por e8group

Qui Jul 19, 2012 20:57
Geometria Plana
-
- Área do Triângulo
por Padoan » Qui Fev 11, 2010 18:36
- 6 Respostas
- 8368 Exibições
- Última mensagem por MarceloFantini

Sex Fev 12, 2010 13:42
Geometria Plana
-
- Área do Triângulo
por Cleyson007 » Sex Mai 14, 2010 13:07
- 1 Respostas
- 2325 Exibições
- Última mensagem por Douglasm

Sex Mai 14, 2010 13:38
Geometria Analítica
-
- Área do Triângulo
por valeuleo » Ter Abr 05, 2011 11:25
- 1 Respostas
- 2691 Exibições
- Última mensagem por LuizAquino

Ter Abr 05, 2011 11:42
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)