 Minha dúvida é quanto a resolução da questão a seguir:
Minha dúvida é quanto a resolução da questão a seguir:(UECE) Se n= (-1/2 sen ?/6 + 1 + sen ?/3 cos ?/6 ) : ( -1/2 cos ?/6 -1 +sen ?/3 sen ?/6), então n² + 1 é igual a :
(A)2 (B) 7/3 (C) 4 (D) 19/3
Eu resolvi deste modo:
sen ?/6 =0,5
sen ?/3 = 0,866
cos ?/6 =0,866
n= (-1/2*0,5 +1 + 0,866*0,866):(-1/2*0,866 -1 + 0,866*0,5)
n= 1,5: (-1)
n= -1,5
Portanto n² + 1 = (-1,5)² +1 = 3,25
No entanto, nehuma das alternativas apresenta esse valor. Em que parte do cálculo eu errei? Já verifiquei se digitei a conta corretamente e revisei cada passo, mas mesmo assim sempre dá o mesmo resultado.
Gostaria que alguem me explicasse a forma correta de resolver esse problema.
Grato


![n = \left[-\frac{1}{2}.sen\left(\frac{\pi}{6} \right) + 1 + sen\left(\frac{\pi}{3} \right).cos\left(\frac{\pi}{6} \right) \right] : n = \left[-\frac{1}{2}.sen\left(\frac{\pi}{6} \right) + 1 + sen\left(\frac{\pi}{3} \right).cos\left(\frac{\pi}{6} \right) \right] :](/latexrender/pictures/a8dbb65f012d904dc225dd8829cee80e.png)
![\left[-\frac{1}{2}.cos\left(\frac{\pi}{6} \right) - 1 + sen\left(\frac{\pi}{3} \right).sen\left(\frac{\pi}{6} \right) \right] \left[-\frac{1}{2}.cos\left(\frac{\pi}{6} \right) - 1 + sen\left(\frac{\pi}{3} \right).sen\left(\frac{\pi}{6} \right) \right]](/latexrender/pictures/befe2841d48a52088d00f6f6dc47479b.png)
![n = \left[-\frac{1}{2}.\frac{1}{2} + 1 + \frac{\sqrt[]{3}}{2}.\frac{\sqrt[]{3}}{2} \right] : n = \left[-\frac{1}{2}.\frac{1}{2} + 1 + \frac{\sqrt[]{3}}{2}.\frac{\sqrt[]{3}}{2} \right] :](/latexrender/pictures/afa4ee51a4f25ec07c5a63d415c0b033.png)
![\left[-\frac{1}{2}.\frac{\sqrt[]{3}}{2} - 1 + \frac{\sqrt[]{3}}{2}.\frac{1}{2} \right] \left[-\frac{1}{2}.\frac{\sqrt[]{3}}{2} - 1 + \frac{\sqrt[]{3}}{2}.\frac{1}{2} \right]](/latexrender/pictures/b00861acc5250a38335fc06bda6d7f55.png)
![n = \left[-\frac{1}{4} + 1 + \frac{3}{4} \right]:\left[-\frac{\sqrt[]{3}}{4} - 1 + \frac{\sqrt[]{3}}{4} \right] n = \left[-\frac{1}{4} + 1 + \frac{3}{4} \right]:\left[-\frac{\sqrt[]{3}}{4} - 1 + \frac{\sqrt[]{3}}{4} \right]](/latexrender/pictures/c8e1f9ca0e3a61f61d6351e4d031c216.png)
![n = \left[1 + \frac{2}{4} \right]:\left[ - 1 \right] n = \left[1 + \frac{2}{4} \right]:\left[ - 1 \right]](/latexrender/pictures/5ecff6ed50c5ac747bc8991e24495e05.png)
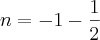



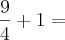
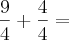
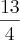

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.