Olá Galerinha.
Tenho dúvida nesta questão:
Se a + b = 180º, então a expressão 1 - sen a * sen b vale:
Resp.: Cos² a
Eu responderia 0; pois se a+b é igual a 180º, então a é igual 90º e b é igual a 90º;
90 + 90 = 180; então 1 - sen 90º * sen 90º seria igual a 0;
mas marca como resposta Cos² a.
Ficarei grato pela ajuda que tiver de alguém.
Obrigado pela atenção.


 se resolve para a = 90 e b = 90, sim sim, mas também se resolve pra a = 1 e b = 179 não é? entre varias outras resoluções a e b não precisam ser iguais
se resolve para a = 90 e b = 90, sim sim, mas também se resolve pra a = 1 e b = 179 não é? entre varias outras resoluções a e b não precisam ser iguais



 então
então 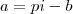 isso é justamente a equaçãozinha que a gente usa pra "transpor" um angulo do primeiro pro segundo quadrante! ficou claro?
isso é justamente a equaçãozinha que a gente usa pra "transpor" um angulo do primeiro pro segundo quadrante! ficou claro? 

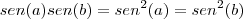



 .
.
 :
: