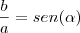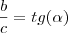por Treblew » Qui Dez 01, 2011 10:47
Ola pessoal meu nome e treblew eu sou novo aqui no forum e me corrija se eu estiver fazendo alguma coisa errada!!!
Pessoal como fazer essa questão?
Determine as medidas x e y indicadas no triangulo retangulo:
Se vcs me ajudarem ficarei muinto grato!!
-
Treblew
- Novo Usuário
-
- Mensagens: 2
- Registrado em: Qui Dez 01, 2011 10:42
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: formado
por TheoFerraz » Qui Dez 01, 2011 11:12
Esse exercicio fica facil se voce conhecer algumas relações simples...
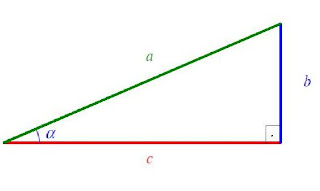
utilizando essas nomeclaturas, as relações são:
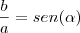
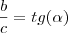
no seu caso temos por exemplo:
tente fazer assim
-
TheoFerraz
- Colaborador Voluntário
-
- Mensagens: 107
- Registrado em: Qua Abr 13, 2011 19:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Física
- Andamento: cursando
por Treblew » Qui Dez 01, 2011 15:24
Obrigado consegui fazer!!!
Sera que ta certo?
Para X:
seno65º = Cateto Oposto / Hipotenusa
0,21 = x / 9
x = 9 . 0,21
x = 1,89
Para Y:
cos65ª = Cateto adjacente / Hipotenusa
0,42= Y/9
Y= 3,78
-
Treblew
- Novo Usuário
-
- Mensagens: 2
- Registrado em: Qui Dez 01, 2011 10:42
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: formado
por TheoFerraz » Qui Dez 01, 2011 21:11
Oh Yeah =)
-
TheoFerraz
- Colaborador Voluntário
-
- Mensagens: 107
- Registrado em: Qua Abr 13, 2011 19:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Física
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Relações no triângulo retângulo
por lucassouza » Sex Jan 16, 2015 20:32
- 1 Respostas
- 1238 Exibições
- Última mensagem por DanielFerreira
Sáb Jan 17, 2015 00:18
Trigonometria
-
- Relações métricas num triângulo retângulo
por Marcampucio » Dom Abr 26, 2009 20:21
- 2 Respostas
- 7636 Exibições
- Última mensagem por Marcampucio
Ter Jun 02, 2009 13:41
Tópicos sem Interação (leia as regras)
-
- relaçoes metricas no triangulo retangulo
por stanley tiago » Dom Jan 23, 2011 18:07
- 2 Respostas
- 2192 Exibições
- Última mensagem por stanley tiago
Dom Jan 23, 2011 22:06
Geometria Plana
-
- [Relações métricas no triângulo Retângulo]
por Gustavo Gomes » Sex Out 26, 2012 21:47
- 1 Respostas
- 2154 Exibições
- Última mensagem por young_jedi
Sex Out 26, 2012 22:08
Geometria Plana
-
- Relações métricas no triângulo retângulo
por Pandaludo » Qua Ago 07, 2013 21:32
- 0 Respostas
- 1012 Exibições
- Última mensagem por Pandaludo
Qua Ago 07, 2013 21:32
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de
Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é
Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:
Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:
Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
