por rodsales » Ter Abr 14, 2009 21:47
por rodsales » Ter Abr 14, 2009 21:47
Bem, estou tendo muitas dificuldades em responder esse exercício, já tentei de várias maneiras, contudo não deu.
-> O triângulo ABC é retângulo em A. Se o seno do ângulo ^B é 0,8, qual o valor da tangente do ângulo ^C?
Grato, esperem que me ajudem...
-

rodsales
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Ter Abr 14, 2009 21:28
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: administração
- Andamento: cursando
 por Molina » Qua Abr 15, 2009 12:04
por Molina » Qua Abr 15, 2009 12:04
Bom dia, Rodsales!
Dado sen(B) = 0,8 é possível calcularmos o cos(B) através da fórmula:

Assim, encontraremos cos(B) = 0,6
Como sen(B) = 0,8

cos(C) = 0,8 e
como cos(B) = 0,6

sen(C) = 0,6.
Agora usamos
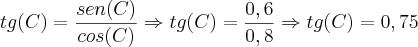
Abraços e bom estudo!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 cos(C) = 0,8 e
cos(C) = 0,8 e