[Equação Trigonométrica]Equação trigonométrica

por **gustavoluiss** » Ter Ago 09, 2011 00:32

$sen x . sec \frac{4\pi}{7} =1$

$cos x . cossec \frac{5\pi}{3} = 1$

$sec x = cossec \frac{3\pi}{8}$

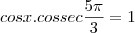
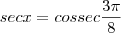
Qual a dica para resolver essas equações trigonométricas ?
Muito Obrigado pela paciência desde de já,

por **LuizAquino** » Ter Ago 09, 2011 20:49

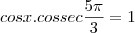
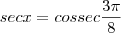
gustavoluiss escreveu:Qual a dica para resolver essas equações trigonométricas ?

A dica é primeiro desenvolver essas equações para obter algo do tipo $\textrm{sen}\,x = \cos y$ .

Em seguida, use o fato de que $\cos y = \textrm{sen}\, \left(\frac{\pi}{2} - y\right)$ .

Sendo assim, você fica com uma equação do tipo $\textrm{sen}\,x = \textrm{sen}\, \left(\frac{\pi}{2} - y\right)$ .

Dessa última equação você obtém que $x = \frac{\pi}{2} - y$ .

Nessa solução estamos considerando que os ângulos

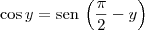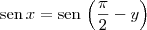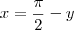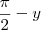e $\frac{\pi}{2} - y$ estão no mesmo quadrante.

Uma solução mais geral é obtida lembrando-se que $\textrm{sen}\,x = \textrm{sen}\,(\pi - x)$ e considerando-se os arcos côngruos.

por **gustavoluiss** » Ter Ago 09, 2011 22:16

ah pocha eu sei, oq eu tentei foi por 1/sen x = sec 4pi / 7 , q daria cossecante x = sec 4pi/7 ,,,, não resolvi me ajuda ?

por **LuizAquino** » Ter Ago 09, 2011 22:47

Vou fazer apenas uma utilizando as dicas dadas anteriormente.

Temos a equação $\textrm{sen}\,x \sec \frac{4\pi}{7} = 1$ .

Aplicando a definição de secante, podemos reescrever essa equação como $\textrm{sen}\,x = \cos \frac{4\pi}{7}$ .

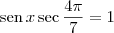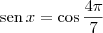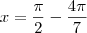Das dicas, segue que no final temos $x = \frac{\pi}{2} - \frac{4\pi}{7}$ . A partir disso, temos que $x = -\frac{\pi}{14}$ .

Lembre-se que um ângulo "negativo" significa apenas que ele foi medido no sentido horário.

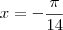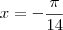Nesse caso o ângulo $x = -\frac{\pi}{14}$ está no quarto quadrante e ele é equivalente a $\frac{27\pi}{14}$ .

Essa é uma solução particular. Para obter a solução geral basta seguir a última parte da dica.

por **gustavoluiss** » Ter Ago 09, 2011 22:49

tava esperando sua respota obrigado,mais que definição da secante se passa pro outro lado como cosseno ?? eu não intendi isso

por **LuizAquino** » Ter Ago 09, 2011 22:53

gustavoluiss escreveu:tava esperando sua respota obrigado,mais que definição da secante se passa pro outro lado como cosseno ?? eu não intendi isso

$\textrm{sen}\,x \sec \frac{4\pi}{7} = 1 \Rightarrow \textrm{sen}\,x \left(\frac{1}{\cos\frac{4\pi}{7}}\right) = 1 \Rightarrow \textrm{sen}\,x = \cos\frac{4\pi}{7}$

por **gustavoluiss** » Ter Ago 09, 2011 22:55

pqp , obrigado as vezes é díficil enxergar algumas coisas simples dessas, ty

por **gustavoluiss** » Ter Ago 09, 2011 22:56

por **gustavoluiss** » Ter Ago 09, 2011 22:57

por **gustavoluiss** » Ter Ago 09, 2011 23:02

ve se sabe essa,

sec x = cossec 3pi /8

por **gustavoluiss** » Ter Ago 09, 2011 23:07

sen 3pi/8 = cos x ???

certo ?

por **LuizAquino** » Qua Ago 10, 2011 08:25

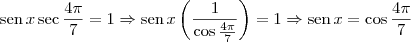
gustavoluiss escreveu:pode me adicionar no msn ?

ou mandar email,pra me acompanhar se eu tiver + alguma dúvida na matéria ?

Não é objetivo do fórum estimular que as dúvidas sejam enviadas por e-maill, mensagem instantânea, mensagem privada ou qualquer outra forma individual.

Lembre-se que a ideia de um fórum é que todos possam se beneficiar com as discussões.

gustavoluiss escreveu:ve se sabe essa,

sec x = cossec 3pi /8

sen 3pi/8 = cos x ???

certo ?

Sim.

por **gustavoluiss** » Qua Ago 10, 2011 18:20

tah certo vlw,

[Equação Trigonométrica]Equação trigonométrica

[Equação Trigonométrica]Equação trigonométrica

[Equação Trigonométrica]Equação trigonométrica

Re: [Equação Trigonométrica]Equação trigonométrica

Re: [Equação Trigonométrica]Equação trigonométrica

Re: [Equação Trigonométrica]Equação trigonométrica

Re: [Equação Trigonométrica]Equação trigonométrica

Re: [Equação Trigonométrica]Equação trigonométrica

Re: [Equação Trigonométrica]Equação trigonométrica

Re: [Equação Trigonométrica]Equação trigonométrica

Re: [Equação Trigonométrica]Equação trigonométrica

Re: [Equação Trigonométrica]Equação trigonométrica

Re: [Equação Trigonométrica]Equação trigonométrica

Re: [Equação Trigonométrica]Equação trigonométrica

Re: [Equação Trigonométrica]Equação trigonométrica

Quem está online