 por Soraya S de Simone » Dom Jun 26, 2011 13:34
por Soraya S de Simone » Dom Jun 26, 2011 13:34
Como simplificar a expressão (cotg x - tg x)/(sec x - cossec x) para 0<x<pi/2
-
Soraya S de Simone
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Dom Jun 26, 2011 13:14
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Dom Jun 26, 2011 14:34
por Molina » Dom Jun 26, 2011 14:34
Boa tarde.
Experimente transformar cada termo em seno e cosseno e verifoque se vai ser possível cancelar algum termo.
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Soraya S de Simone » Dom Jun 26, 2011 19:20
por Soraya S de Simone » Dom Jun 26, 2011 19:20
Desenvolvi a expressão: ((cos x/sen x) - (sen x/cos x)) / ((1/cos x) - (1/sen x)) = ((cos ao quadrado de x - sen ao quadrado de x) / (sen x X cos x)) / ((sen x - cos x) / (sen x X cos x)) = (cos ao quadrado de x - sen ao quadrado de x) / (sen x - cos x)
A partir daí não consegui simplificar mais.
-
Soraya S de Simone
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Dom Jun 26, 2011 13:14
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por FilipeCaceres » Dom Jun 26, 2011 19:57
por FilipeCaceres » Dom Jun 26, 2011 19:57
Você encontrou
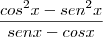
Então faça o seguinte,
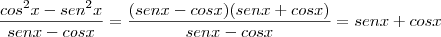
Utilize o latex para postar suas dúvidas leia
viewtopic.php?f=9&t=74
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [trigonometria] trigonometria em triangulo qualquer
por biamassa00 » Sex Mai 25, 2012 22:19
- 0 Respostas
- 3597 Exibições
- Última mensagem por biamassa00

Sex Mai 25, 2012 22:19
Trigonometria
-
- (Trigonometria) problema trigonometria
por Luizap11 » Qui Dez 05, 2013 00:33
- 2 Respostas
- 5276 Exibições
- Última mensagem por Edunclec

Qui Dez 05, 2013 20:53
Trigonometria
-
- trigonometria
por Cleyson007 » Qua Set 24, 2008 19:44
- 2 Respostas
- 3416 Exibições
- Última mensagem por admin

Ter Set 30, 2008 19:08
Trigonometria
-
- trigonometria
por Micheline » Dom Jan 25, 2009 16:21
- 5 Respostas
- 4967 Exibições
- Última mensagem por Cleyson007

Seg Jan 26, 2009 17:27
Trigonometria
-
- Trigonometria
por Flavio » Sex Fev 13, 2009 21:29
- 5 Respostas
- 5129 Exibições
- Última mensagem por Molina

Seg Fev 16, 2009 01:53
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





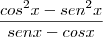
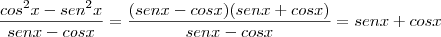

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.