Questão Mackenzie

por **Guilherme Carvalho** » Sex Mai 13, 2011 12:24

Num retângulo de lados 1cm e 3cm, o menor seno do ângulo formado pelas diagonais é:

a)4/5
b)3/5
c)1/5
d)1/3
e)2/5

por **carlosalesouza** » Sex Mai 13, 2011 16:47

Primeiramente, encontrando as diagonais:

$\\a^2=b^2+c^2\\ a^2=1^2+3^2\\ a^2=1+9\\ a^2=10\\ a=\sqrt{10}$

Agora, sabemos que o menor seno pertence ao ângulo que possua menor cateto oposto, ou seja, pegaremos o ângulo voltado para o lado menor...

Contudo, para termos um triângulo retângulo, vamos cortá-lo ao meio, então seu lado oposto será a metade do ângulo original...

Sabemos que as diagonais se cruzam em seu ponto médio... Assim as medidas desse triângulo retângulo são:

$a=\frac{\sqrt{10}}{2},\ b=\frac{1}{2},\ c=?$

Assim:
$\\ \left(\frac{\sqrt{10}}{2}\right)^2=\left(\frac{1}{2}\right)^2+c^2\\ \frac{10}{4} = \frac{1}{4}+c^2\\ c^2=\frac{10-1}{4}\\ c=\sqrt{\frac{9}{4}}\\ c=\frac{3}{2}$

Pra encontrar o seno, basta b/a... mas esse ângulo é a metade do ângulo que queremos... então sen(2x)

E sabemos que sen(2x) = 2(senx.cosx)

Então precisamos achar o coseno tbm...

O seno:
$\\ sen = \frac{\frac{1}{2}}{\frac{\sqrt{10}}{2}}=\frac{1}{2}\cdot\frac{2}{\sqrt{10}}=\frac{1}{\sqrt{10}}=\frac{\sqrt{10}}{10}$

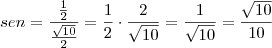
O coseno:
$cos = \frac{\frac{3}{2}}{\frac{\sqrt{10}}{2}}=\frac{3}{\sqrt{10}}=\frac{3\sqrt{10}}{10}$

Agora podemos fazer

$sen(2x)=2\left(sen(x).cos(x)\right)=2\left(\frac{\sqrt{10}}{10}\cdot\frac{3\sqrt{10}}{10}}\right)=2\left(\frac{30}{100}\right) =\frac{6}{10}=\frac{3}{5}$

Portanto, a respostá é B

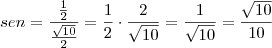
Questão Mackenzie

Questão Mackenzie

Questão Mackenzie

Re: Questão Mackenzie

Quem está online