Através da soma dos ângulos internor do triangulo, conclui que o ângulo D^B^C também é 45°. E através da relação envolvendo sen 45°, conclui que um dos catetos vale
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) , já que os catetos de um triângulo retângulo com os outros dois ângulos de 45° tem que ter mesmo valor, os dois serão
, já que os catetos de um triângulo retângulo com os outros dois ângulos de 45° tem que ter mesmo valor, os dois serão ![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) . Só consigo até aqui. Mas a professora, teima que tem como achar o perímetro só com isso... Imaginei fazer por semelhança, mas nem tentei, porque ela disse que só poderiamos usar sen, cos e tg ou teorema de pitágoras. Bom é isso. Espero que alguém saiba resolver ou então me aponte erros ou qualquer coisa do tipo. Desde já agradeço!
. Só consigo até aqui. Mas a professora, teima que tem como achar o perímetro só com isso... Imaginei fazer por semelhança, mas nem tentei, porque ela disse que só poderiamos usar sen, cos e tg ou teorema de pitágoras. Bom é isso. Espero que alguém saiba resolver ou então me aponte erros ou qualquer coisa do tipo. Desde já agradeço!Forte abraço.
Giles.



 , sem considerar o ângulo
, sem considerar o ângulo 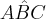 reto.
reto.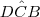 ,
, 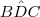 ,
, 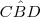 e os segmentos
e os segmentos  ,
,  e
e  :
: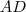 .
.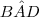 e
e 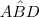 se alteram, assim como o próprio segmento
se alteram, assim como o próprio segmento 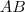 .
.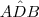 que também é reto).
que também é reto).
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)