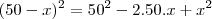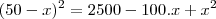por tiagofe » Qui Mar 31, 2011 20:09
por tiagofe » Qui Mar 31, 2011 20:09

Boa tarde pessoal, estou com um duvida que está me matando!
segue a imagem onde esta o problema.
http://postimage.org/image/drrc8lwk/ou está em
http://www.freeimagehosting.net/image.p ... fff57c.jpgja tentei de todas as maneiras mas não chego a resoluçao certa, no livro a resposta da
17.1) é as torres 1 e 2 distam do lago 18 pés e 32 pés respectivamente.
17.2) alpha = 43.15º beta 82.39º
não encontro relação nenguma com a distancia 50 com a hipotenusa dos triangulos ( distancia em que os pombos percorreram.)
penso que as hipotenusas são iguais pois os pombos chegaram ao mesmo tempo.
alguem me de uma ajuda

Muito Obrigado.
-
tiagofe
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Qui Mar 31, 2011 19:50
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: matematica
- Andamento: cursando
 por FilipeCaceres » Qui Mar 31, 2011 20:25
por FilipeCaceres » Qui Mar 31, 2011 20:25
Vou lhe dar uma dica, observe a figura abaixo (fora de escala).Como os dois pássaros tem a mesma velocidade, eles vão levar o mesmo tempo até atingir o solo, então ambos percorrem a mesma distância d. Aplicando pitágoras nos dois triângulo e igualando d, você descobrirá quanto vale x.

- torres.GIF (2.29 KiB) Exibido 5976 vezes
Se tiver mais alguma dúvida compartilhe conosco.
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por tiagofe » Qui Mar 31, 2011 20:35
por tiagofe » Qui Mar 31, 2011 20:35
filipecaceres escreveu:Vou lhe dar uma dica, observe a figura abaixo (fora de escala).Como os dois pássaros tem a mesma velocidade, eles vão levar o mesmo tempo até atingir o solo, então ambos percorrem a mesma distância d. Aplicando pitágoras nos dois triângulo e igualando d, você descobrirá quanto vale x.
torres.GIF
Se tiver mais alguma dúvida compartilhe conosco.
Abraço.
Muito Obrigado pela rapida resposta, aqui ja é tarde e estou cansado para analisar bem o problema, mas acho que ja chego la sozinho, amanha de manha volto a força!

muito obrigado mais uma vez

-
tiagofe
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Qui Mar 31, 2011 19:50
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: matematica
- Andamento: cursando
 por Elcioschin » Qui Mar 31, 2011 22:47
por Elcioschin » Qui Mar 31, 2011 22:47
Existe um erro no gabarito ----> Beta ~= 65,77º
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por tiagofe » Sex Abr 01, 2011 07:25
por tiagofe » Sex Abr 01, 2011 07:25
Muito Obrigado a todos, vou postar a minha resolução os resultados batem certo mas qualquer erro que detectarem digam para eu corrigir
http://img190.imageshack.us/i/img015tr.jpg/ aqui está.
PS. desculpem a letra mas a culpa é do scanner!

-
tiagofe
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Qui Mar 31, 2011 19:50
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: matematica
- Andamento: cursando
 por Elcioschin » Sex Abr 01, 2011 12:05
por Elcioschin » Sex Abr 01, 2011 12:05
Existem vários erros na sua solução: você elevou (50 - x) ao quadrado de forma indevida.
d² = 40² + x² ----> d = 1600 + x²
d² = 30² + (50 - x)² ----> d² = 900 + 2500 - 100x + x² ----> d² = 3400 - 100x + x²
1600 + x² = 3400 - 100x + x²
100x = 3400 - 1600
100x = 1800
x = 18
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por tiagofe » Sex Abr 01, 2011 13:09
por tiagofe » Sex Abr 01, 2011 13:09
Elcioschin escreveu:Existem vários erros na sua solução: você elevou (50 - x) ao quadrado de forma indevida.
d² = 40² + x² ----> d = 1600 + x²
d² = 30² + (50 - x)² ----> d² = 900 + 2500 - 100x + x² ----> d² = 3400 - 100x + x²
1600 + x² = 3400 - 100x + x²
100x = 3400 - 1600
100x = 1800
x = 18
Boa tarde Elcioschin
não entendi a parte do
-100x de onde vc tirou esse valor?
Muito Obrigado.
-
tiagofe
- Usuário Ativo

-
- Mensagens: 17
- Registrado em: Qui Mar 31, 2011 19:50
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: matematica
- Andamento: cursando
 por FilipeCaceres » Sex Abr 01, 2011 13:15
por FilipeCaceres » Sex Abr 01, 2011 13:15
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- fibonacci
por GehSillva7 » Dom Fev 28, 2016 18:16
- 0 Respostas
- 1057 Exibições
- Última mensagem por GehSillva7

Dom Fev 28, 2016 18:16
Aritmética
-
- Indução Finita FIbonacci
por Garota nerd » Ter Mai 03, 2011 17:52
- 3 Respostas
- 2969 Exibições
- Última mensagem por Garota nerd

Qui Mai 05, 2011 00:43
Álgebra Elementar
-
- Problema
por fabio muniz » Qui Out 23, 2008 16:14
- 1 Respostas
- 10723 Exibições
- Última mensagem por admin

Ter Out 28, 2008 17:47
Problemas do Cotidiano
-
- Problema
por Lima » Dom Dez 14, 2008 18:08
- 3 Respostas
- 9734 Exibições
- Última mensagem por blangis

Dom Dez 14, 2008 20:15
Sistemas de Equações
-
- Problema..
por ANDRE RENATO PROFETA » Sex Mar 13, 2009 00:36
- 1 Respostas
- 3318 Exibições
- Última mensagem por Molina

Sex Mar 13, 2009 14:58
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.