estou com dúvidas em duas questões: 1. Se sec
 =
=![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) e
e , então
, então  é igual a:
é igual a:já tentei passar para sen e cos, para depois voltar à sec, mas não deu certo:
 =
=
È por aí?
2. O gráfico da função definida por f(x)=x2 + bx + c
 R, em que c=cos
R, em que c=cos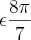
a) intercepta o eixo das abscissas em exatamente 2 pontos positivos
b) intercepta o eixo das abscissas em exatamente 2 pontos negativos
c) intercepta o eixo das abscisas em 2 pontos de sinais diferentes
d) intercepta o eixo das abscissas na origem
e) não intercepta o eixo das abscissas.
Essa não sei nem por onde começo.


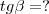


 ).
).
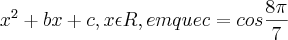 .
.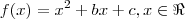 , em que
, em que 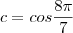
 . Escreva-o e pense como será o sinal dele.
. Escreva-o e pense como será o sinal dele. é do 3º quadrante! E que um número ao quadrado é sempre positivo.
é do 3º quadrante! E que um número ao quadrado é sempre positivo. em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.