 por PedroSantos » Qua Dez 01, 2010 18:40
por PedroSantos » Qua Dez 01, 2010 18:40
Num triângulo retângulo sabe-se que a medida do catedo adjacente ao angulo

é de 4, a medida do cateto oposto é 5 e a
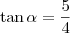
.
Pertende-se determinar a amplitude do ângulo

(em graus).
Sei que nas máquinas calculadoras existe a tecla
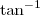
, no entanto gostaria de saber como resolver este problema de uma forma algébrica.
Obrigado
-
PedroSantos
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qua Dez 01, 2010 16:38
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: ensino secundário
- Andamento: cursando
 por Elcioschin » Qui Dez 02, 2010 13:53
por Elcioschin » Qui Dez 02, 2010 13:53
A solução algébrica é impossível, pois o valor do ângulo é um número irracional.
Existem 3 modos de calcular um valor aproximado:
1) Calculadora ou Excel
2) Tabela de seno cosseno e tangente para ânglos entre 0º e 90º
3) Uso de séries (matéria do curso superior):
arctgx = tg^-1(x) = x¹/1! - x³/3! + x^5/5! - x^7/7! + ....... = x - x³/6 + x^5/120 - x^7/5040 + ......
Basta agora fazer x = 5/4
Editado pela última vez por
Elcioschin em Qui Dez 02, 2010 15:48, em um total de 1 vez.
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por PedroSantos » Qui Dez 02, 2010 14:46
por PedroSantos » Qui Dez 02, 2010 14:46
Obrigado pela orientação.
-
PedroSantos
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qua Dez 01, 2010 16:38
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: ensino secundário
- Andamento: cursando
 por Elcioschin » Qui Dez 02, 2010 15:48
por Elcioschin » Qui Dez 02, 2010 15:48
Pedro
Fiz uma pequena complementação.
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Calculos envolvendo triângulo retângulo e retângulo
 por andersontricordiano » Seg Abr 18, 2011 02:29
por andersontricordiano » Seg Abr 18, 2011 02:29
- 1 Respostas
- 4036 Exibições
- Última mensagem por MarceloFantini

Seg Abr 18, 2011 04:19
Progressões
-
- Triangulo Retangulo
por ginrj » Qui Jun 04, 2009 18:56
- 1 Respostas
- 3410 Exibições
- Última mensagem por ginrj

Seg Jun 15, 2009 18:14
Geometria Plana
-
- Triângulo retângulo
por DanielFerreira » Qua Jul 29, 2009 15:38
- 5 Respostas
- 6831 Exibições
- Última mensagem por Cleyson007

Qui Jul 30, 2009 17:22
Trigonometria
-
- Triângulo retangulo
por cristina » Seg Set 21, 2009 14:56
- 3 Respostas
- 2205 Exibições
- Última mensagem por DanielFerreira

Ter Set 22, 2009 14:18
Trigonometria
-
- Triângulo retângulo
por DanielFerreira » Qui Mar 03, 2011 11:26
- 1 Respostas
- 2124 Exibições
- Última mensagem por Elcioschin

Qui Mar 03, 2011 14:43
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 é de 4, a medida do cateto oposto é 5 e a
é de 4, a medida do cateto oposto é 5 e a 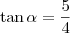 .
. (em graus).
(em graus).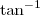 , no entanto gostaria de saber como resolver este problema de uma forma algébrica.
, no entanto gostaria de saber como resolver este problema de uma forma algébrica.
 é de 4, a medida do cateto oposto é 5 e a
é de 4, a medida do cateto oposto é 5 e a 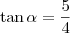 .
. (em graus).
(em graus).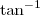 , no entanto gostaria de saber como resolver este problema de uma forma algébrica.
, no entanto gostaria de saber como resolver este problema de uma forma algébrica.



 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.