por Adriano De Souza » Ter Nov 02, 2010 16:32
por Adriano De Souza » Ter Nov 02, 2010 16:32
PRECISO DE UMA AJUDA AE PESSOAL!
estou cursando o ensino medio tec. materia nova um trabalho e nao estou conseguindo chega a lugar algum!
PRESISO DO
RESULTADO I DA RESOLUÇAO!
1) Sendo 0

x < 2

A) Sen X =
![\sqrt[]{2}/2 \sqrt[]{2}/2](/latexrender/pictures/8450365496cb8076b83d7e1458c1a146.png)
B) Cos X = -
![\frac{\sqrt[]{3}}{2} \frac{\sqrt[]{3}}{2}](/latexrender/pictures/21682d7c1e802e9b52a99c01850489c4.png)
C) Sen x = -1
D) Cos X = -1
-
Adriano De Souza
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Ter Nov 02, 2010 16:11
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Andamento: cursando
 por Neperiano » Ter Nov 02, 2010 18:38
por Neperiano » Ter Nov 02, 2010 18:38
Ola
Não sei se entendi mas acho que voce quer converter estes numeros para graus
Então voce deve usar a arc sen, sendo assim primeiro obtenha o valor com virgula, por exemplo
raiz de 2/2 igual 0,70
Voce quer saber o seno de 0,70, então use
sen-1 0,70 = 45 que para saber em termo de pi deve usar regra de 3
pi - 180
x - 45
x - pi/4
Mas isso é usando calculadora, sem usar ela eu não sei mas acredito que deve dar pra fazer
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por andrefahl » Qua Nov 03, 2010 03:52
por andrefahl » Qua Nov 03, 2010 03:52
Bom, acho que o enunciado num deve ter sido postado na integra neh...
mas pelo que eu entendi ele está pergunta qual angulo no intervalo de
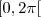
que o seno ou o cosseno assume esses valores.
daí sim, use a explicação do Lúcio para resolver.
Lembrando que seno e cosseno são funções periodicas e por isso
as vezes vc terá mais de angulo um mm valor de seno ou cosseno.
ah e tb verifique o intervalo se esta correto x<2pi e naum menor ou igual...
nesse caso vc terá apenas um valor para x no sen x = 1 =)
-
andrefahl
- Usuário Dedicado

-
- Mensagens: 36
- Registrado em: Qui Out 28, 2010 18:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física - UNICAMP
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [trigonometria] trigonometria em triangulo qualquer
por biamassa00 » Sex Mai 25, 2012 22:19
- 0 Respostas
- 3591 Exibições
- Última mensagem por biamassa00

Sex Mai 25, 2012 22:19
Trigonometria
-
- (Trigonometria) problema trigonometria
por Luizap11 » Qui Dez 05, 2013 00:33
- 2 Respostas
- 5267 Exibições
- Última mensagem por Edunclec

Qui Dez 05, 2013 20:53
Trigonometria
-
- Urgente
por jean » Ter Nov 25, 2008 18:39
- 2 Respostas
- 2478 Exibições
- Última mensagem por jean

Ter Nov 25, 2008 21:36
Pedidos
-
- urgente!!
 por weverton » Qui Jul 29, 2010 19:38
por weverton » Qui Jul 29, 2010 19:38
- 4 Respostas
- 3807 Exibições
- Última mensagem por weverton

Sáb Jul 31, 2010 22:47
Estatística
-
- urgente!!
por matematicada » Qui Nov 25, 2010 11:52
- 2 Respostas
- 2067 Exibições
- Última mensagem por Elcioschin

Qui Nov 25, 2010 16:11
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 x < 2
x < 2
![\sqrt[]{2}/2 \sqrt[]{2}/2](/latexrender/pictures/8450365496cb8076b83d7e1458c1a146.png)
![\frac{\sqrt[]{3}}{2} \frac{\sqrt[]{3}}{2}](/latexrender/pictures/21682d7c1e802e9b52a99c01850489c4.png)

 x < 2
x < 2
![\sqrt[]{2}/2 \sqrt[]{2}/2](/latexrender/pictures/8450365496cb8076b83d7e1458c1a146.png)
![\frac{\sqrt[]{3}}{2} \frac{\sqrt[]{3}}{2}](/latexrender/pictures/21682d7c1e802e9b52a99c01850489c4.png)