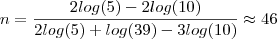por Louis » Seg Jul 09, 2012 17:59
por Louis » Seg Jul 09, 2012 17:59
Olá, estou estudando matemática para obter um desempenho satisfatório no vestibular. Agradeço a ajuda.
Uma pessoa adquiriu uma calça jeans e observou que ela perde 2,5% de sua cor a cada lavagem, de tal modo que, após n lavagens, terá apenas 25% de sua cor original. Considerando, se necessário, log 5 = 0,698 e log 39 = 1,591, pode-se estimar que o valor aproximado de n é:
01) 10
02) 19
03) 28
04) 37
05) 46
Fazendo uma regra de três básica marquei 10 como sendo a resposta, mas o gabarito afirma que é 46.
-
Louis
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Seg Jul 09, 2012 17:48
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por e8group » Seg Jul 09, 2012 20:16
por e8group » Seg Jul 09, 2012 20:16
Seja Z a cor (C) da da calça ,após a primeira lavagem temos :
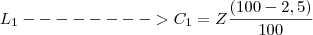
Na segunda temos :
![L_2 --------> C_2 = C_1\frac{ (100 - 2,5 )}{100}= Z\left[\frac{ (100 - 2,5 )}{100} \right]^2 L_2 --------> C_2 = C_1\frac{ (100 - 2,5 )}{100}= Z\left[\frac{ (100 - 2,5 )}{100} \right]^2](/latexrender/pictures/533ddebba6ca81a6cf0a3a78821c2b93.png)
generalizando temos :
![L_n --------> C_n = C_{n-1}\frac{ (100 - 2,5 )}{100} = Z\left[\frac{ (100 - 2,5 )}{100} \right]^n L_n --------> C_n = C_{n-1}\frac{ (100 - 2,5 )}{100} = Z\left[\frac{ (100 - 2,5 )}{100} \right]^n](/latexrender/pictures/7b0acc492195171677fa479eb7995e7a.png)
,como

então ,
![Z\left[\frac{ (100 - 2,5 )}{100} \right]^n = \frac{25}{100} Z Z\left[\frac{ (100 - 2,5 )}{100} \right]^n = \frac{25}{100} Z](/latexrender/pictures/08cf233f5af9b01a52452f5a6e5f462e.png)
. Aplicando Logaritmo de base 10 em ambos membros da equação temos :

, ou seja
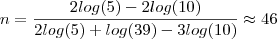
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Louis » Seg Jul 09, 2012 22:59
por Louis » Seg Jul 09, 2012 22:59
Muito obrigado, Santhiago!

-
Louis
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Seg Jul 09, 2012 17:48
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [logaritmo]dúvida sobre logaritmo
por tigocma » Ter Mar 25, 2014 22:43
- 0 Respostas
- 1847 Exibições
- Última mensagem por tigocma

Ter Mar 25, 2014 22:43
Logaritmos
-
- Duvida Logaritmo
por Xyko » Qua Mar 03, 2010 09:21
- 2 Respostas
- 2063 Exibições
- Última mensagem por MarceloFantini

Qui Mar 04, 2010 21:53
Logaritmos
-
- Logaritmo - {dúvida}
por Danilo » Dom Ago 26, 2012 08:38
- 2 Respostas
- 1296 Exibições
- Última mensagem por Danilo

Dom Ago 26, 2012 19:28
Logaritmos
-
- Duvida Logaritmo
por Ana_0305 » Dom Out 14, 2012 21:05
- 1 Respostas
- 1156 Exibições
- Última mensagem por MarceloFantini

Dom Out 14, 2012 21:11
Logaritmos
-
- Dúvida logaritmo
por leandropressato » Seg Abr 15, 2013 10:58
- 1 Respostas
- 2978 Exibições
- Última mensagem por DanielFerreira

Seg Abr 15, 2013 18:15
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


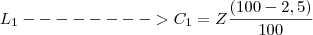
![L_2 --------> C_2 = C_1\frac{ (100 - 2,5 )}{100}= Z\left[\frac{ (100 - 2,5 )}{100} \right]^2 L_2 --------> C_2 = C_1\frac{ (100 - 2,5 )}{100}= Z\left[\frac{ (100 - 2,5 )}{100} \right]^2](/latexrender/pictures/533ddebba6ca81a6cf0a3a78821c2b93.png)
![L_n --------> C_n = C_{n-1}\frac{ (100 - 2,5 )}{100} = Z\left[\frac{ (100 - 2,5 )}{100} \right]^n L_n --------> C_n = C_{n-1}\frac{ (100 - 2,5 )}{100} = Z\left[\frac{ (100 - 2,5 )}{100} \right]^n](/latexrender/pictures/7b0acc492195171677fa479eb7995e7a.png) ,como
,como  então ,
então ,![Z\left[\frac{ (100 - 2,5 )}{100} \right]^n = \frac{25}{100} Z Z\left[\frac{ (100 - 2,5 )}{100} \right]^n = \frac{25}{100} Z](/latexrender/pictures/08cf233f5af9b01a52452f5a6e5f462e.png) . Aplicando Logaritmo de base 10 em ambos membros da equação temos :
. Aplicando Logaritmo de base 10 em ambos membros da equação temos : , ou seja
, ou seja