1) Simplificar

Essa eu não tive e idéia nem por onde começar, pensei em tentar mudar de base, mas não deu certo... praticamente não saí do zero. Log dentro de log é uma coisa muito estranha para mim, existe alguma regra prática para esse tipo de situação?
Resposta:

Consegui resolver a primeira, era bobeira, elevei 10 a log a ( já que estava dividindo)
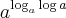 podendo assim simplificar para
podendo assim simplificar para 
2) Se
 e
e 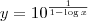 prove que:
prove que: 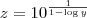
Como cada uma das definições depende da outra eu fiquei perdido ao tentar unificá-las, sem sucesso também. Como faço para isolar uma incógnita em uma situação dessas?
3) Resolver a equação

Utilizando as propriedades e transformando tudo em log ficou assim:
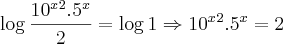
Resposta: -1 e log 2
Por enquanto são só essas, tentando refazer meus passos acabei conseguindo algumas que não havia conseguido antes.
Obrigado pela atenção



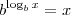 , temos que:
, temos que:
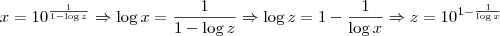



 , temos que:
, temos que:
 .
.