 por santiago alves » Sex Jul 15, 2011 00:13
por santiago alves » Sex Jul 15, 2011 00:13
Olá galera...
Estou estudando por este livro na esperaça de conseguir acompanhar o curso de calculo...
Bem, minha duvida é como faço pra resolver estes exercícios::
5-) log2^x . ln(x) + ln(x-2) = 0
6-) 35=(1+x)4
8-) (2^(3x+1))/(3^(2x-1))=5^x
creio que com as resoluções destes o restante, dos exercicios ficaram mais claros!!!
desde ja agradeço...
-
santiago alves
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qua Abr 20, 2011 11:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Claudin » Sex Jul 15, 2011 00:18
por Claudin » Sex Jul 15, 2011 00:18
Editado pela última vez por
Claudin em Sex Jul 15, 2011 01:36, em um total de 1 vez.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por santiago alves » Sex Jul 15, 2011 00:40
por santiago alves » Sex Jul 15, 2011 00:40
Perdão pelo inconviniente....
a primeira formula eu escrevi errado, as demais estao de acordo com a forma expressa no livro...
esta é a formula certa!!!!
5-)

É motivante saber que existe um suporte de tao alto nível disponível na internet aos que realmente tem o interesse de aprender a arte da matemática....
Meu problema em sí, esta em uma parte da resoluçao dessa eq. logaritmica:
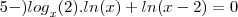

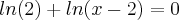
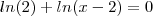
não sei oq fazer com o "ln(x-2)" e ainda nao encontrei resposta na net e nem exemplos desse tipo mais detalhados...
se alguem tiver paciencia pra explicar um pouco mais detalhado seria de grande ajuda mesmo!!!
vlws!!!!
-
santiago alves
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qua Abr 20, 2011 11:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por LuizAquino » Sex Jul 15, 2011 10:44
por LuizAquino » Sex Jul 15, 2011 10:44
santiago alves escreveu: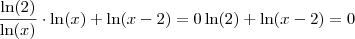
Imagine que você tenha um número n diferente de zero. Quanto vale a fração

? Ora, isso vale 1! Desse modo, o correto seria escrever:

Tome cuidado com as simplificações!
Agora, você tem a equação:

Para resolvê-la eu vou dar uma dica. Lembre-se da propriedade de logaritmos que diz que:
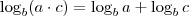
Aproveito também para lhe dar mais duas dicas:
- Para fazer uma revisão dos conteúdos do ensino fundamental ou médio, um bom lugar para começar é o canal do Nerckie no YouTube:
http://www.youtube.com/nerckie
- Se você desejar assistir um curso no YouTube sobre Cálculo Diferencial e Integral I, então eu espero que o meu canal possa ajudar:
http://www.youtube.com/LCMAquino
Observaçãosantiago alves escreveu:Livro: Matematica basica para ensino Superior. LOGARITMOS
Olá galera...
Estou estudando por este livro na esperaça de conseguir acompanhar o curso de calculo...
Bem, esse é um livro muito básico para um aluno do curso de engenharia. Procure não passar muito tempo utilizando ele como referência. É recomendado que você use um livro como, por exemplo, Cálculo Vol. 1 de James Stewart.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Livro: Matematica basica para ensino Superior. pg. 59 ex4
por santiago alves » Ter Jul 12, 2011 13:45
- 2 Respostas
- 2374 Exibições
- Última mensagem por santiago alves

Ter Jul 12, 2011 14:23
Sistemas de Equações
-
- Livro: Matematica basica para ensino fundamental. pg. 55 ex1
 por santiago alves » Sex Jul 08, 2011 08:46
por santiago alves » Sex Jul 08, 2011 08:46
- 2 Respostas
- 2888 Exibições
- Última mensagem por santiago alves

Sex Jul 08, 2011 10:46
Polinômios
-
- [Gráficos de funções]matemática do ensino superior
por Breno94 » Dom Abr 12, 2015 22:13
- 1 Respostas
- 2497 Exibições
- Última mensagem por nakagumahissao

Dom Jul 19, 2015 11:59
Funções
-
- [DICA] Livro de Matemática Ensino Fundamental
por invader_zim » Seg Fev 11, 2013 14:54
- 9 Respostas
- 9610 Exibições
- Última mensagem por alex_08

Ter Fev 12, 2013 18:01
Álgebra Elementar
-
- [Probabilidade Ensino Superior]
por yuricastilho » Sáb Abr 19, 2014 20:16
- 1 Respostas
- 3123 Exibições
- Última mensagem por paulo testoni

Dom Jun 29, 2014 00:14
Probabilidade
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




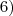
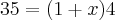
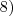
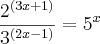


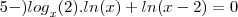

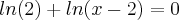
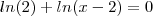
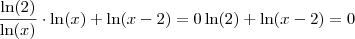
 ? Ora, isso vale 1! Desse modo, o correto seria escrever:
? Ora, isso vale 1! Desse modo, o correto seria escrever:

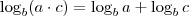

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.