 por natanskt » Sáb Out 09, 2010 15:00
por natanskt » Sáb Out 09, 2010 15:00
29-)(AFA) sendo
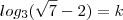
o valor de

é:
a-)1-k
b-)1+k
c-)2-k
d-)2+k
-
natanskt
- Colaborador Voluntário

-
- Mensagens: 176
- Registrado em: Qua Out 06, 2010 14:56
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: nenhum
- Andamento: cursando
 por Douglasm » Sáb Out 09, 2010 17:29
por Douglasm » Sáb Out 09, 2010 17:29
Primeiramente, há um erro no enunciado: Queremos o valor de

, que não é igual a
k. Chamarei esse valor de
x. Assim temos:

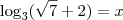
Multiplicando um pelo outro temos:


Ficamos com a
letra a.
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação logaritmica
por DanielRJ » Qui Out 07, 2010 17:20
- 4 Respostas
- 2472 Exibições
- Última mensagem por DanielRJ

Sáb Out 09, 2010 15:28
Logaritmos
-
- (AFA) equação logaritmica
por natanskt » Sex Out 08, 2010 12:27
- 2 Respostas
- 1877 Exibições
- Última mensagem por Molina

Sex Out 08, 2010 14:30
Funções
-
- (AFA) equação logaritmica
por natanskt » Sex Out 08, 2010 12:30
- 1 Respostas
- 1462 Exibições
- Última mensagem por DanielRJ

Sex Out 08, 2010 14:13
Funções
-
- (AFA) Equação logaritmica
por natanskt » Sáb Out 09, 2010 13:31
- 1 Respostas
- 1676 Exibições
- Última mensagem por DanielRJ

Sáb Out 09, 2010 13:42
Logaritmos
-
- (AFA) Equação logaritmica
por natanskt » Sáb Out 09, 2010 14:51
- 2 Respostas
- 1826 Exibições
- Última mensagem por natanskt

Seg Out 11, 2010 15:58
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
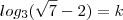 o valor de
o valor de  é:
é:
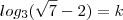 o valor de
o valor de  é:
é:
 , que não é igual a k. Chamarei esse valor de x. Assim temos:
, que não é igual a k. Chamarei esse valor de x. Assim temos:
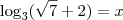



 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.