 por thamysoares » Sex Nov 16, 2012 10:01
por thamysoares » Sex Nov 16, 2012 10:01
A partir de um certo ano, a população de uma cidade passou a crescer de acordo com a função
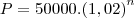
em que n representa os anos e P, o número de habitantes. Sabendo-se que log1,02=0,009, depois de quantos anos aproximadamente essa cidade atingirá 500000 habitantes?
Me expliquem como se resolve questões desse tipo, por favor. Obg.
-
thamysoares
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Qua Nov 14, 2012 19:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Sex Nov 16, 2012 11:48
por e8group » Sex Nov 16, 2012 11:48
Bom dia , thamysoares . Esta função

denota o números de habitantes em função do tempo

, a medida que o tempo

vai aumentando ,o número de habitantes cresce estritamente . Neste caso particular , o exercício que vc calcule o tempo

que satisfaz o número de habitantes .

.
Basta resolver ,
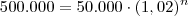
.Consegue terminar ?
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por thamysoares » Sex Nov 16, 2012 15:44
por thamysoares » Sex Nov 16, 2012 15:44
santhiago escreveu:Bom dia , thamysoares . Esta função

denota o números de habitantes em função do tempo

, a medida que o tempo

vai aumentando ,o número de habitantes cresce estritamente . Neste caso particular , o exercício que vc calcule o tempo

que satisfaz o número de habitantes .

.
Basta resolver ,
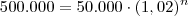
.Consegue terminar ?
Deu aproximadamente 111 anos. Está correto?
-
thamysoares
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Qua Nov 14, 2012 19:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Sex Nov 16, 2012 16:12
por e8group » Sex Nov 16, 2012 16:12
Isso mesmo , estar correto
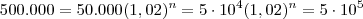
Multiplicando ambos lados por

vem que ,

.
Aplicando logaritmo ,
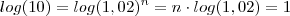
Pelo enunciado ,
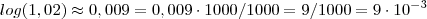
Daí ,
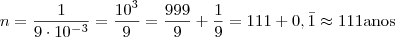
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por thamysoares » Sex Nov 16, 2012 16:34
por thamysoares » Sex Nov 16, 2012 16:34
santhiago escreveu:Isso mesmo , estar correto
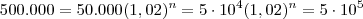
Multiplicando ambos lados por

vem que ,

.
Aplicando logaritmo ,
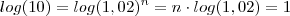
Pelo enunciado ,
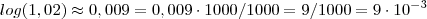
Daí ,
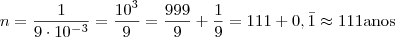
Obrigada Santhiago!! =)
-
thamysoares
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Qua Nov 14, 2012 19:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
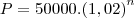 em que n representa os anos e P, o número de habitantes. Sabendo-se que log1,02=0,009, depois de quantos anos aproximadamente essa cidade atingirá 500000 habitantes?
em que n representa os anos e P, o número de habitantes. Sabendo-se que log1,02=0,009, depois de quantos anos aproximadamente essa cidade atingirá 500000 habitantes?
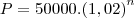 em que n representa os anos e P, o número de habitantes. Sabendo-se que log1,02=0,009, depois de quantos anos aproximadamente essa cidade atingirá 500000 habitantes?
em que n representa os anos e P, o número de habitantes. Sabendo-se que log1,02=0,009, depois de quantos anos aproximadamente essa cidade atingirá 500000 habitantes?
 denota o números de habitantes em função do tempo
denota o números de habitantes em função do tempo  , a medida que o tempo
, a medida que o tempo  vai aumentando ,o número de habitantes cresce estritamente . Neste caso particular , o exercício que vc calcule o tempo
vai aumentando ,o número de habitantes cresce estritamente . Neste caso particular , o exercício que vc calcule o tempo  que satisfaz o número de habitantes .
que satisfaz o número de habitantes .  .
. 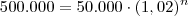 .Consegue terminar ?
.Consegue terminar ?
denota o números de habitantes em função do tempo
, a medida que o tempo
vai aumentando ,o número de habitantes cresce estritamente . Neste caso particular , o exercício que vc calcule o tempo
que satisfaz o número de habitantes .
.
.Consegue terminar ?

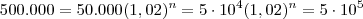
 vem que ,
vem que ,  .
. 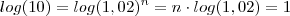
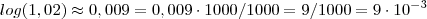
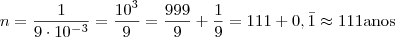

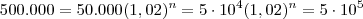
vem que ,
.
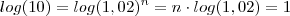

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
