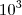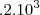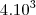por natanskt » Qua Out 13, 2010 18:09
por natanskt » Qua Out 13, 2010 18:09
18-)a intensidade (i) de um terremoto em uma determinada escala,é definida por

,em que E é a energia instatanea liberada pelo terremoto,cuja a duração foi de 8segundos,variou em função do tempo conforme a equação

,t em segundos e i em kwh,no instante em que a intensidade do terremoto era maxima,a energia liberada,em kwh,era de
a-)

b-)
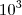
c-)
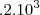
d-)

e-)
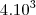
-
natanskt
- Colaborador Voluntário

-
- Mensagens: 176
- Registrado em: Qua Out 06, 2010 14:56
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: nenhum
- Andamento: cursando
 por natanskt » Sex Out 15, 2010 12:12
por natanskt » Sex Out 15, 2010 12:12
ajuda aí galera
abraços
-
natanskt
- Colaborador Voluntário

-
- Mensagens: 176
- Registrado em: Qua Out 06, 2010 14:56
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: nenhum
- Andamento: cursando
 por gustavofr » Qui Out 28, 2010 09:19
por gustavofr » Qui Out 28, 2010 09:19
Estava faltando dizer que E0 = 10^-3!
A intensidade máxima:
i(t) = -t²/4 + 2t
imáx = - ?/4ª --> -(b² - 4ac)/4ª --> -(2² - 4*(-1/4)*0)/4*(-1/4)
imáx = -4/-1 = 4
Aplicando em i = (2/3)log(E/E0)
4 = (2/3)log(E/10^-3) --> 6 = log E – Log 10^-3 --> 6 = logE + 3
3 = LogE --> E = 10³.
Letra B
-
gustavofr
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Qui Out 28, 2010 09:08
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (ESPCEX) Equação logaritmica
por natanskt » Seg Out 11, 2010 16:16
- 3 Respostas
- 2185 Exibições
- Última mensagem por MarceloFantini

Qua Out 13, 2010 13:50
Logaritmos
-
- (ESPCEX) Equação logaritmica
por natanskt » Seg Out 11, 2010 16:23
- 3 Respostas
- 1758 Exibições
- Última mensagem por DanielRJ

Seg Out 11, 2010 18:39
Logaritmos
-
- (ESPCEX) Equação logaritmica
por natanskt » Seg Out 11, 2010 16:50
- 2 Respostas
- 5658 Exibições
- Última mensagem por DanielRJ

Seg Out 11, 2010 18:25
Logaritmos
-
- (ESPCEX) Equação logaritmica
por natanskt » Seg Out 11, 2010 16:53
- 3 Respostas
- 2948 Exibições
- Última mensagem por MarceloFantini

Qui Out 14, 2010 16:38
Logaritmos
-
- (ESPCEX) função logaritmica
por natanskt » Sex Out 29, 2010 10:34
- 1 Respostas
- 1573 Exibições
- Última mensagem por SidneySantos

Qua Abr 20, 2011 20:36
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 ,em que E é a energia instatanea liberada pelo terremoto,cuja a duração foi de 8segundos,variou em função do tempo conforme a equação
,em que E é a energia instatanea liberada pelo terremoto,cuja a duração foi de 8segundos,variou em função do tempo conforme a equação  ,t em segundos e i em kwh,no instante em que a intensidade do terremoto era maxima,a energia liberada,em kwh,era de
,t em segundos e i em kwh,no instante em que a intensidade do terremoto era maxima,a energia liberada,em kwh,era de