 por natanskt » Seg Out 11, 2010 16:53
por natanskt » Seg Out 11, 2010 16:53
considerando
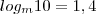
e
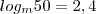
,pode-se afirmar que,com base nesses dados,que o valor do logaritmo decimal de 5 é:
a-)3/7
b-)1/2
c-)5/7
d-)7/3
e-)7/5
-
natanskt
- Colaborador Voluntário

-
- Mensagens: 176
- Registrado em: Qua Out 06, 2010 14:56
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: nenhum
- Andamento: cursando
 por MarceloFantini » Seg Out 11, 2010 17:40
por MarceloFantini » Seg Out 11, 2010 17:40
Veja que
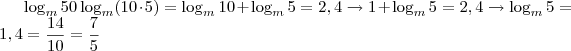
Alternativa E.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por natanskt » Qui Out 14, 2010 10:48
por natanskt » Qui Out 14, 2010 10:48
olá fantini
o gabarito aqui esta falando que é a alternativa C
já encontrei erros no gabarito,mais pode ver certinho se vc não esqueceu de nada:?
ABRAÇOS AMIGO
-
natanskt
- Colaborador Voluntário

-
- Mensagens: 176
- Registrado em: Qua Out 06, 2010 14:56
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: nenhum
- Andamento: cursando
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (ESPCEX) Equação logaritmica
por natanskt » Seg Out 11, 2010 16:16
- 3 Respostas
- 2185 Exibições
- Última mensagem por MarceloFantini

Qua Out 13, 2010 13:50
Logaritmos
-
- (ESPCEX) Equação logaritmica
por natanskt » Seg Out 11, 2010 16:23
- 3 Respostas
- 1758 Exibições
- Última mensagem por DanielRJ

Seg Out 11, 2010 18:39
Logaritmos
-
- (ESPCEX) Equação logaritmica
por natanskt » Seg Out 11, 2010 16:50
- 2 Respostas
- 5657 Exibições
- Última mensagem por DanielRJ

Seg Out 11, 2010 18:25
Logaritmos
-
- (ESPCEX) Equação logaritmica
por natanskt » Qua Out 13, 2010 18:09
- 2 Respostas
- 4839 Exibições
- Última mensagem por gustavofr

Qui Out 28, 2010 09:19
Logaritmos
-
- (ESPCEX) função logaritmica
por natanskt » Sex Out 29, 2010 10:34
- 1 Respostas
- 1573 Exibições
- Última mensagem por SidneySantos

Qua Abr 20, 2011 20:36
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
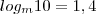 e
e 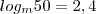 ,pode-se afirmar que,com base nesses dados,que o valor do logaritmo decimal de 5 é:
,pode-se afirmar que,com base nesses dados,que o valor do logaritmo decimal de 5 é:
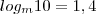 e
e 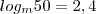 ,pode-se afirmar que,com base nesses dados,que o valor do logaritmo decimal de 5 é:
,pode-se afirmar que,com base nesses dados,que o valor do logaritmo decimal de 5 é:


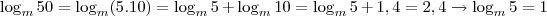

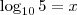 ) .
) .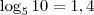 .
.




 .
.



