 por Sandy26 » Sex Abr 23, 2010 14:12
por Sandy26 » Sex Abr 23, 2010 14:12
oi
Preciso mesmo ajuda para resolver este exercicio
Função g, real de variavel real
g(x) =log e (2x-e^2)-2
a) dominio e contradominio da Função g
b) Calcule aso esistam os zeros de g
c) Mostra k g é continua em x=e^2?
D) Calcule, caso existe o valor de lim qd x tende +00 g´(x).
Consegui resolver
a) ]e^2;+00[
D´g =R
b) resutado deu me x=e^2
Ajudam me por favor a resolver a c e D
-
Sandy26
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Sex Abr 23, 2010 13:53
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Andamento: cursando
 por Sandy26 » Sex Abr 23, 2010 17:27
por Sandy26 » Sex Abr 23, 2010 17:27
oi estive a tentar resolver será que esta certo
preg d)
log e (2x-e^2)-2 = y
= log e (2x-e^2 = y + 2
= 2x-e^2= e^y+2
= 2x= e^y+2 + e^2
= x= e^y+2 + e^2/2
Acham que esta certo
Podem me dar uma pistas para fazer a pregunta c?
-
Sandy26
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Sex Abr 23, 2010 13:53
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Andamento: cursando
 por Molina » Sex Abr 23, 2010 19:34
por Molina » Sex Abr 23, 2010 19:34
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Sandy26 » Sáb Abr 24, 2010 06:22
por Sandy26 » Sáb Abr 24, 2010 06:22
Obrigada por ajuda
Olha uma duvida k me ficou loge e é igual sempre a 1?
-
Sandy26
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Sex Abr 23, 2010 13:53
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Andamento: cursando
 por MarceloFantini » Sáb Abr 24, 2010 06:39
por MarceloFantini » Sáb Abr 24, 2010 06:39
Em geral,
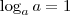
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Sandy26 » Sáb Abr 24, 2010 19:11
por Sandy26 » Sáb Abr 24, 2010 19:11
Obrigada agora já entendo
Acham que estou a fazer bem este exercico
Monstra k a função h atinge um minimum em X=3
h(x)= |3-x|
Fazo a derivada do modulo
h`(x) =-1 se x >3
1 se x<3
Dá me
Fazendo um quatro:
-oo a 3 sinal -
3 sinal + +00
-
Sandy26
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Sex Abr 23, 2010 13:53
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Andamento: cursando
 por MarceloFantini » Dom Abr 25, 2010 02:36
por MarceloFantini » Dom Abr 25, 2010 02:36
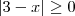
. Então

ou
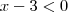
. O único que atinge um valor mínimo é a primeira opção, quando

.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Sandy26 » Seg Abr 26, 2010 10:45
por Sandy26 » Seg Abr 26, 2010 10:45
ok !!!! Mas para saber o mimino não se ten k fazer a derivada e depois fazer o quadro com os sinal para saber se é cresente o decresente!!
Acham k tenho certo
Inequação Resolver: -3x^2 -3x + 18<0
Utilizou a formula resolvente
x= -(-3) +-V(3)^2+4*(-3)*18 / 2*(-3)
x= 3 +- V 9 + (216) / -6
x= 3 +- V-207 /6
Inequação imposivel
please ajudam tenho teste para semana e estou cheia de duvidas!!!
-
Sandy26
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Sex Abr 23, 2010 13:53
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Andamento: cursando
 por MarceloFantini » Seg Abr 26, 2010 14:44
por MarceloFantini » Seg Abr 26, 2010 14:44
Sandy, por favor evite colocar mais de uma pergunta no mesmo tópico. Já colocou a de módulo (o que não deveria) e agora colocou outra. Por favor crie um tópico novo para cada pergunta.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Sandy26 » Ter Abr 27, 2010 14:56
por Sandy26 » Ter Abr 27, 2010 14:56
Como possou fazer para saber o dominio e contradominio de uma função com log?
-
Sandy26
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Sex Abr 23, 2010 13:53
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Andamento: cursando
 por Sandy26 » Qui Abr 29, 2010 15:15
por Sandy26 » Qui Abr 29, 2010 15:15
Please ajudam a preceber melhor o dominio e contradominio!!!
-
Sandy26
- Usuário Ativo

-
- Mensagens: 16
- Registrado em: Sex Abr 23, 2010 13:53
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Andamento: cursando
 por Molina » Qui Abr 29, 2010 17:42
por Molina » Qui Abr 29, 2010 17:42
Sandy26 escreveu:Como possou fazer para saber o dominio e contradominio de uma função com log?
O que estiver depois do log tem que ser maior que zero. Este será o domínio.
E o contradomínio são todos os reais.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por MarceloFantini » Qui Abr 29, 2010 17:57
por MarceloFantini » Qui Abr 29, 2010 17:57
Pense na definição de domínio, contra-domínio e da função logarítmica.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- ajuda por favor
por zeramalho2004 » Dom Abr 05, 2009 21:31
- 3 Respostas
- 8656 Exibições
- Última mensagem por zeramalho2004

Seg Abr 06, 2009 10:25
Logaritmos
-
- ajuda por favor !!!
por Moacir » Qui Ago 27, 2009 00:19
- 2 Respostas
- 2726 Exibições
- Última mensagem por Moacir

Qui Ago 27, 2009 17:30
Funções
-
- Ajuda, por favor!
por Dimas » Sex Set 24, 2010 23:16
- 2 Respostas
- 1845 Exibições
- Última mensagem por Rogerio Murcila

Qua Set 29, 2010 15:51
Trigonometria
-
- Ajuda por favor.
por Josiebruno » Qua Out 20, 2010 09:36
- 0 Respostas
- 1124 Exibições
- Última mensagem por Josiebruno

Qua Out 20, 2010 09:36
Álgebra Elementar
-
- Ajuda, por favor !
por Luciana Dias » Qui Mar 22, 2012 20:24
- 1 Respostas
- 1650 Exibições
- Última mensagem por joaofonseca

Qui Mar 22, 2012 21:33
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




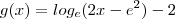
 temos:
temos:
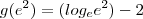
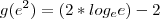

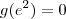





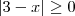 . Então
. Então  ou
ou 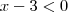 . O único que atinge um valor mínimo é a primeira opção, quando
. O único que atinge um valor mínimo é a primeira opção, quando  .
.










![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)