 por adauto martins » Sex Out 18, 2019 18:04
por adauto martins » Sex Out 18, 2019 18:04
(escola de aeronautica-exame ad.1943)
resolver a equaçao
![log\sqrt[]{7x+3}+log\sqrt[]{4x+5}=(1/2)+log3 log\sqrt[]{7x+3}+log\sqrt[]{4x+5}=(1/2)+log3](/latexrender/pictures/95b5fa431d75545c9bb8d37b2c0ac7ff.png)
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Sex Out 18, 2019 18:18
por adauto martins » Sex Out 18, 2019 18:18
soluçao:
![log\sqrt[]{7x+3}+log\sqrt[]{4x+5}=(1/2)+log3 log\sqrt[]{7x+3}+log\sqrt[]{4x+5}=(1/2)+log3](/latexrender/pictures/95b5fa431d75545c9bb8d37b2c0ac7ff.png)
![log\sqrt[]{7x+3}+log\sqrt[]{4x+5}-log3=(1/2)
log((\sqrt[]{7x+3}).(\sqrt[]{4x+5})/3)=(1/2)
(\sqrt[]{7x+3}).(\sqrt[]{4x+5})/3=\sqrt[]{10}
(7x+3).(4x+5)=90... log\sqrt[]{7x+3}+log\sqrt[]{4x+5}-log3=(1/2)
log((\sqrt[]{7x+3}).(\sqrt[]{4x+5})/3)=(1/2)
(\sqrt[]{7x+3}).(\sqrt[]{4x+5})/3=\sqrt[]{10}
(7x+3).(4x+5)=90...](/latexrender/pictures/3949e41d7568c0421d6bb7dbd6b2fd00.png)
resolvendo a equaçao do 2º grau,teremos as raizes
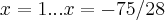

nao pode ser soluçao(pq?)
logo

...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![log\sqrt[]{7x+3}+log\sqrt[]{4x+5}=(1/2)+log3 log\sqrt[]{7x+3}+log\sqrt[]{4x+5}=(1/2)+log3](/latexrender/pictures/95b5fa431d75545c9bb8d37b2c0ac7ff.png)

![log\sqrt[]{7x+3}+log\sqrt[]{4x+5}=(1/2)+log3 log\sqrt[]{7x+3}+log\sqrt[]{4x+5}=(1/2)+log3](/latexrender/pictures/95b5fa431d75545c9bb8d37b2c0ac7ff.png)

![log\sqrt[]{7x+3}+log\sqrt[]{4x+5}=(1/2)+log3 log\sqrt[]{7x+3}+log\sqrt[]{4x+5}=(1/2)+log3](/latexrender/pictures/95b5fa431d75545c9bb8d37b2c0ac7ff.png)
![log\sqrt[]{7x+3}+log\sqrt[]{4x+5}-log3=(1/2)
log((\sqrt[]{7x+3}).(\sqrt[]{4x+5})/3)=(1/2)
(\sqrt[]{7x+3}).(\sqrt[]{4x+5})/3=\sqrt[]{10}
(7x+3).(4x+5)=90... log\sqrt[]{7x+3}+log\sqrt[]{4x+5}-log3=(1/2)
log((\sqrt[]{7x+3}).(\sqrt[]{4x+5})/3)=(1/2)
(\sqrt[]{7x+3}).(\sqrt[]{4x+5})/3=\sqrt[]{10}
(7x+3).(4x+5)=90...](/latexrender/pictures/3949e41d7568c0421d6bb7dbd6b2fd00.png)
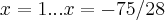
 nao pode ser soluçao(pq?)
nao pode ser soluçao(pq?) ...
...

 .
.



