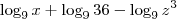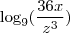por pereirajoaojr » Dom Nov 02, 2014 17:25
por pereirajoaojr » Dom Nov 02, 2014 17:25
Reduza a expressão dada em um único logaritmo:
log9 x + log3 6 - 3log9 z
Me ajudem por favor
-
pereirajoaojr
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Nov 02, 2014 17:17
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por adauto martins » Seg Nov 03, 2014 17:43
por adauto martins » Seg Nov 03, 2014 17:43
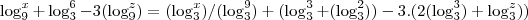
=
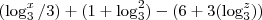
=
![(\log_{3}^{x}/3)-3\log_{3}^{z}+\log_{3}^{2}-5=\log_{3}^{2(\sqrt[3]{x})/(({z}^{3})(\sqrt[5]{3}))} (\log_{3}^{x}/3)-3\log_{3}^{z}+\log_{3}^{2}-5=\log_{3}^{2(\sqrt[3]{x})/(({z}^{3})(\sqrt[5]{3}))}](/latexrender/pictures/322c56424442435d43bc951946b3289a.png)
...costumo errar em contas,mas o racionio e esse...confere ai
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por pereirajoaojr » Ter Nov 04, 2014 01:32
por pereirajoaojr » Ter Nov 04, 2014 01:32
No gabarito marca que a resposta é log9 (36x/z³), mas não consigo chegar nesse resultado.
-
pereirajoaojr
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Dom Nov 02, 2014 17:17
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por Russman » Ter Nov 04, 2014 13:49
por Russman » Ter Nov 04, 2014 13:49
Primeiro reduza todos os logaritmos a mesma base. Lembre-se que
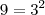
de modo que, segundo a identidade
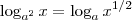
temos
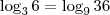
.
Ainda,
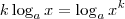
. Portanto,
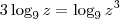
. Assim, sua expressão fica
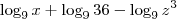
que é, segundo as propriedades de soma e diferença de logaritmos,
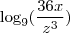
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- para cada vetor V o simétrico -V é único
por dkiwilson » Sáb Set 23, 2017 19:16
- 0 Respostas
- 2587 Exibições
- Última mensagem por dkiwilson

Sáb Set 23, 2017 19:16
Álgebra Linear
-
- Prove que cada inteiro "a" tem um unico oposto
por zero » Dom Mar 08, 2009 20:43
- 2 Respostas
- 2259 Exibições
- Última mensagem por zero

Qua Mar 11, 2009 22:02
Álgebra Elementar
-
- DADA A FUNÇÃO
por SILMARAKNETSCH » Sex Nov 09, 2012 15:29
- 5 Respostas
- 2822 Exibições
- Última mensagem por SILMARAKNETSCH

Sex Nov 09, 2012 16:50
Funções
-
- Dada a matriz seu determinante é:
por oescolhido » Qua Fev 20, 2013 18:40
- 1 Respostas
- 3026 Exibições
- Última mensagem por young_jedi

Qua Fev 20, 2013 21:08
Matrizes e Determinantes
-
- Problema com Derivada dada Implicitamente
por Loretto » Qui Jul 29, 2010 17:15
- 2 Respostas
- 5148 Exibições
- Última mensagem por Loretto

Sex Jul 30, 2010 15:00
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



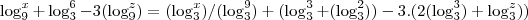 =
=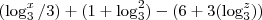 =
=![(\log_{3}^{x}/3)-3\log_{3}^{z}+\log_{3}^{2}-5=\log_{3}^{2(\sqrt[3]{x})/(({z}^{3})(\sqrt[5]{3}))} (\log_{3}^{x}/3)-3\log_{3}^{z}+\log_{3}^{2}-5=\log_{3}^{2(\sqrt[3]{x})/(({z}^{3})(\sqrt[5]{3}))}](/latexrender/pictures/322c56424442435d43bc951946b3289a.png) ...costumo errar em contas,mas o racionio e esse...confere ai
...costumo errar em contas,mas o racionio e esse...confere ai

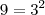 de modo que, segundo a identidade
de modo que, segundo a identidade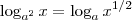
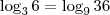 .
.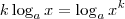 . Portanto,
. Portanto, 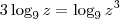 . Assim, sua expressão fica
. Assim, sua expressão fica