e 
calcular ![log \sqrt[4]{60}](/latexrender/pictures/08c35f52c72b882e326c056c1705cc9e.png "log \sqrt[4]{60}")
fiz da seguinte forma: primeiro fatorei
ficando da seguinte forma![log \sqrt[3]{{2}^{2}.3.5}](/latexrender/pictures/d71731d45747a120550de62860652375.png "log \sqrt[3]{{2}^{2}.3.5}")
retirei todos da raiz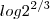 
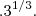
tombei os expoentes e someis tudo -> 
( conseiderando 
) cheguei a os seguintes resultados: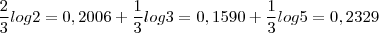 
tudo isso eu encontrei 
porem o correto resultado é 
sei que a diferença é pouca, mas como esse log faz parte de uma conta maior no final ficou mto diferente, por favor alguem me ajude, não encontro meu erro, desde já agradeço.
![log\sqrt[3]{60} = \frac{1}{3}\left(log60 \right) = \frac{1}{3}log\left(10.2.3 \right) = \frac{1}{3}\left(log10 + log2 + log3 \right) = \frac{1}{3} \left(1 + 0,3010 + 0,4771 \right)](/latexrender/pictures/f9ea99a5db637cf97afc3d5f0202e9c5.png "log\sqrt[3]{60} = \frac{1}{3}\left(log60 \right) = \frac{1}{3}log\left(10.2.3 \right) = \frac{1}{3}\left(log10 + log2 + log3 \right) = \frac{1}{3} \left(1 + 0,3010 + 0,4771 \right)")
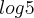que citou estava mesmo no enunciado?
por 
.
: