 por JKS » Dom Mar 17, 2013 13:32
por JKS » Dom Mar 17, 2013 13:32
Não estou conseguindo achar , por favor se alguém puder me ajugar agradeço.
(puc)Sendo x e y número reais positivos tais que
![log {x}^{2}.\sqrt[]{y} &= log2+1 \\
x-\sqrt[]{y} &= -3 log {x}^{2}.\sqrt[]{y} &= log2+1 \\
x-\sqrt[]{y} &= -3](/latexrender/pictures/e777eaa57174bdcb88ddc4e7f06eb425.png)
o produto xy é igual a : GABARITO = 50
-
JKS
- Usuário Parceiro

-
- Mensagens: 53
- Registrado em: Qua Ago 01, 2012 13:13
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por DanielFerreira » Dom Mar 17, 2013 18:34
por DanielFerreira » Dom Mar 17, 2013 18:34
Equação I:
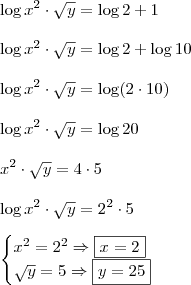
Por conseguinte,

"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Sistema de Logaritmo
por AnakinGabriel » Sáb Mar 09, 2013 20:15
- 1 Respostas
- 1411 Exibições
- Última mensagem por e8group

Sáb Mar 09, 2013 21:46
Logaritmos
-
- [Derivada de Logaritmo Natural] Exercício de logaritmo
por Ronaldobb » Dom Out 28, 2012 17:40
- 1 Respostas
- 2572 Exibições
- Última mensagem por MarceloFantini

Dom Out 28, 2012 18:16
Cálculo: Limites, Derivadas e Integrais
-
- [logaritmo]dúvida sobre logaritmo
por tigocma » Ter Mar 25, 2014 22:43
- 0 Respostas
- 1850 Exibições
- Última mensagem por tigocma

Ter Mar 25, 2014 22:43
Logaritmos
-
- [sistema linear homogeneo] Como resolver esse sistema
por amigao » Qua Jul 02, 2014 14:49
- 1 Respostas
- 3091 Exibições
- Última mensagem por Russman

Qua Jul 02, 2014 18:38
Álgebra Linear
-
- [Sistema Linear] MACK-SP: Sistema de Equações
por ALF » Sex Ago 26, 2011 13:24
- 1 Respostas
- 4496 Exibições
- Última mensagem por LuizAquino

Dom Ago 28, 2011 12:57
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![log {x}^{2}.\sqrt[]{y} &= log2+1 \\
x-\sqrt[]{y} &= -3 log {x}^{2}.\sqrt[]{y} &= log2+1 \\
x-\sqrt[]{y} &= -3](/latexrender/pictures/e777eaa57174bdcb88ddc4e7f06eb425.png)

![log {x}^{2}.\sqrt[]{y} &= log2+1 \\
x-\sqrt[]{y} &= -3 log {x}^{2}.\sqrt[]{y} &= log2+1 \\
x-\sqrt[]{y} &= -3](/latexrender/pictures/e777eaa57174bdcb88ddc4e7f06eb425.png)

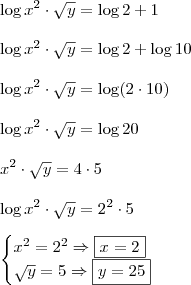




 , avisa que eu resolvo.
, avisa que eu resolvo.

