 por crsjcarlos » Qui Dez 06, 2012 10:42
por crsjcarlos » Qui Dez 06, 2012 10:42
Para que valores de x, x

[0 , 2

] verifica-se a desigualdade:

+

> 1
Resposta:

< x <

ou
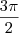
< x <
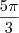
-
crsjcarlos
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qua Dez 05, 2012 17:32
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por e8group » Qui Dez 06, 2012 17:58
por e8group » Qui Dez 06, 2012 17:58
Pela condição de existência

.Uma vez que

.Assim obtemos o seguinte intervalo ,

. Desenvolvendo a inequação ,
![log_{cos(x)}(cos(x)+1) + log_{cos(x)}(2 cos(x)+1)> 1 \\ \implies log_{cos(x)}[(cos(x)+1)(2 cos(x)+1)] > 1 = log_{cos(x)}(cos(x)) log_{cos(x)}(cos(x)+1) + log_{cos(x)}(2 cos(x)+1)> 1 \\ \implies log_{cos(x)}[(cos(x)+1)(2 cos(x)+1)] > 1 = log_{cos(x)}(cos(x))](/latexrender/pictures/7c54790752a18582a827a04a389ac69f.png)
.
Assim ,
![(cos(x)+1)(2 cos(x)+1) > cos(x) \implies 2cos^2(x) + 2cos(x) + 1 > 0 \implies 2 cos(x)[cos(x)+1]> -1 (cos(x)+1)(2 cos(x)+1) > cos(x) \implies 2cos^2(x) + 2cos(x) + 1 > 0 \implies 2 cos(x)[cos(x)+1]> -1](/latexrender/pictures/a8863ee6fa5619d8b1d904ad96cd4941.png)
.
Conclusão :
Como ,

vamos ter

.Logo ,
![2 cos(x)[cos(x)+1] > 0 , \forall x \in (0,\pi/2) \cup (3\pi/2,2\pi) 2 cos(x)[cos(x)+1] > 0 , \forall x \in (0,\pi/2) \cup (3\pi/2,2\pi)](/latexrender/pictures/f20cf26f82cb7738d73fcc01bca3b382.png)
e portanto
![2 cos(x)[cos(x)+1] > - 1 2 cos(x)[cos(x)+1] > - 1](/latexrender/pictures/7845dad4060eaed44ede2cd71a21c089.png)
.
Não sei como chegar no gabarito .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- inequação Logarítmica 2°EM
por Beik » Sex Out 22, 2010 13:28
- 3 Respostas
- 2376 Exibições
- Última mensagem por DanielRJ

Sex Out 22, 2010 15:56
Logaritmos
-
- (AFA) inequação logaritmica
por natanskt » Sex Out 29, 2010 10:49
- 2 Respostas
- 3209 Exibições
- Última mensagem por MarceloFantini

Qui Nov 04, 2010 10:33
Logaritmos
-
- (AFA) inequação logaritmica
por natanskt » Sex Out 29, 2010 10:54
- 2 Respostas
- 2045 Exibições
- Última mensagem por Pedro123

Seg Nov 01, 2010 20:59
Logaritmos
-
- Inequação Logarítmica
por Rafael16 » Sex Ago 10, 2012 11:36
- 1 Respostas
- 1578 Exibições
- Última mensagem por e8group

Sex Ago 10, 2012 12:22
Logaritmos
-
- [Inequação Logaritmica]
por Gustavo Gomes » Sex Fev 07, 2014 22:28
- 1 Respostas
- 1559 Exibições
- Última mensagem por e8group

Sáb Fev 08, 2014 09:58
Inequações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 [0 , 2
[0 , 2 ] verifica-se a desigualdade:
] verifica-se a desigualdade: +
+  > 1
> 1 < x <
< x <  ou
ou 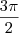 < x <
< x < 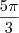

 [0 , 2
[0 , 2 ] verifica-se a desigualdade:
] verifica-se a desigualdade: +
+  > 1
> 1 < x <
< x <  ou
ou 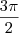 < x <
< x < 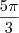

 .Uma vez que
.Uma vez que  .Assim obtemos o seguinte intervalo ,
.Assim obtemos o seguinte intervalo ,  . Desenvolvendo a inequação ,
. Desenvolvendo a inequação , ![log_{cos(x)}(cos(x)+1) + log_{cos(x)}(2 cos(x)+1)> 1 \\ \implies log_{cos(x)}[(cos(x)+1)(2 cos(x)+1)] > 1 = log_{cos(x)}(cos(x)) log_{cos(x)}(cos(x)+1) + log_{cos(x)}(2 cos(x)+1)> 1 \\ \implies log_{cos(x)}[(cos(x)+1)(2 cos(x)+1)] > 1 = log_{cos(x)}(cos(x))](/latexrender/pictures/7c54790752a18582a827a04a389ac69f.png) .
. ![(cos(x)+1)(2 cos(x)+1) > cos(x) \implies 2cos^2(x) + 2cos(x) + 1 > 0 \implies 2 cos(x)[cos(x)+1]> -1 (cos(x)+1)(2 cos(x)+1) > cos(x) \implies 2cos^2(x) + 2cos(x) + 1 > 0 \implies 2 cos(x)[cos(x)+1]> -1](/latexrender/pictures/a8863ee6fa5619d8b1d904ad96cd4941.png) .
.  vamos ter
vamos ter  .Logo ,
.Logo , ![2 cos(x)[cos(x)+1] > 0 , \forall x \in (0,\pi/2) \cup (3\pi/2,2\pi) 2 cos(x)[cos(x)+1] > 0 , \forall x \in (0,\pi/2) \cup (3\pi/2,2\pi)](/latexrender/pictures/f20cf26f82cb7738d73fcc01bca3b382.png) e portanto
e portanto ![2 cos(x)[cos(x)+1] > - 1 2 cos(x)[cos(x)+1] > - 1](/latexrender/pictures/7845dad4060eaed44ede2cd71a21c089.png) .
.


 , avisa que eu resolvo.
, avisa que eu resolvo.

