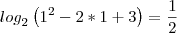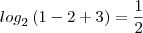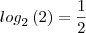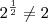Boa tarde Molina, o exercicio completo é o seguinte.
Resolva a equação
(I) a solução da equação

é x= 12
(II) é x = 1 faz parte da solução
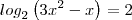
(III) a solução da equação
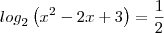
é x= 1
conforme as respostas encontradas p/ as queso~es acima. è correto que:
a) todas estão corretas
b) apenas a sentença II é correta
c) as sentenças I e III são corretas
d) nenhuma sentença está correta...
Olha já verifiquei um milhão de vezes e não tem nada copiado errado....o q esta me matando é que as duas primeiras na minha opiniao estao corretas, certo? mas a ultima, não consigo e as alternativas não batem com as respostas encontradas, por isso estou precisando de ajuda...
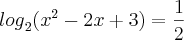 é x = 1
é x = 1

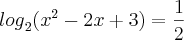 é x = 1
é x = 1
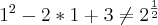


 é x= 12
é x= 12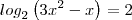
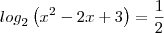 é x= 1
é x= 1
 é x= 12 ?
é x= 12 ?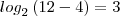
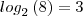

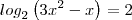
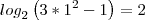


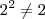
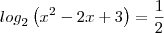 é x= 1
é x= 1