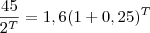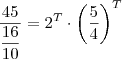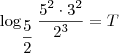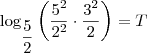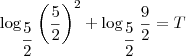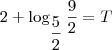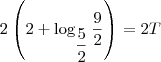por saulfiterman » Seg Ago 20, 2012 21:26
por saulfiterman » Seg Ago 20, 2012 21:26
Questão 45 do vestibular da baiana de medicina 2012.2 :
Consegui resolver apenas a parte da matemática financeira mas não consegui desenvolver o logaritmo para chegar na resposta correta. Peço encarecidamente a ajuda de alguém para resolver essa questão.
Enquanto uma lâmpada incandescente converte em luz apenas 5% de energia elétrica que consome, as de LED converte até 40%, trazendo benefícios evidentes ao meio ambiente. O único inconveniente é o fato de a lâmpada de LED ainda custar mais caro - US$45,00 - apesar de seu preço cair pela metade a cada dois anos.
Admitindo-se que uma lâmpada halógena incandescente custa US$1,60 e tem seu preço aumentado em 25% a cada dois anos, pode-se estimar que os dois tipos de lâmpada serão vendidos pelo mesmo valor, em um tempo t anos, que pode ser aproximado pela expressão :
A alternativa correta da questão é 04) 2(2 + log(9/2) na base 5/2)
PS. : não consegui transformar a equação do log através do programa Latex mas espero que esteja compreensível.
Obrigado
-
saulfiterman
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Seg Ago 20, 2012 20:44
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LuizAquino » Seg Set 24, 2012 10:50
por LuizAquino » Seg Set 24, 2012 10:50
saulfiterman escreveu:Questão 45 do vestibular da baiana de medicina 2012.2 :
Consegui resolver apenas a parte da matemática financeira mas não consegui desenvolver o logaritmo para chegar na resposta correta. Peço encarecidamente a ajuda de alguém para resolver essa questão.
Enquanto uma lâmpada incandescente converte em luz apenas 5% de energia elétrica que consome, as de LED converte até 40%, trazendo benefícios evidentes ao meio ambiente. O único inconveniente é o fato de a lâmpada de LED ainda custar mais caro - US$45,00 - apesar de seu preço cair pela metade a cada dois anos.
Admitindo-se que uma lâmpada halógena incandescente custa US$1,60 e tem seu preço aumentado em 25% a cada dois anos, pode-se estimar que os dois tipos de lâmpada serão vendidos pelo mesmo valor, em um tempo t anos, que pode ser aproximado pela expressão :
A alternativa correta da questão é 04) 2(2 + log(9/2) na base 5/2)
Considere aqui que T é um período de 2 anos. Desse modo, T = 1 representa 2 anos. Já T = 2 representa 4 anos. E assim sucessivamente.
Pelos dados da questão, temos temos que a cada período T o valor da lâmpada de LED será
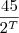
. Por outro lado, a cada período T o valor da lâmpada incandescente será

. Desejamos descobrir para que período t esses valores serão iguais. Temos então que:
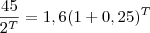
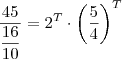


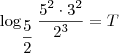
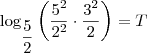
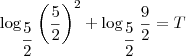
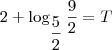
Lembrando então que T aqui representa um período de 2 anos, como o exercício pede o valor em anos, temos que dobrar esse valor de T, obtendo assim:
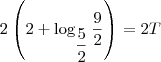
saulfiterman escreveu:PS. : não consegui transformar a equação do log através do programa Latex mas espero que esteja compreensível.
Obrigado
Bastaria usar o código:
- Código: Selecionar todos
[tex]2\left(2 + \log_{\dfrac{5}{2}} \dfrac{9}{2}\right)[/tex]
Como você já viu na reposta acima, o resultado desse código será:

-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Matemática Financeira - Questão com Porcentagem
por joedsonazevedo » Qui Nov 08, 2012 14:50
- 6 Respostas
- 6746 Exibições
- Última mensagem por saberdigitalnet

Sáb Nov 24, 2012 21:01
Matemática Financeira
-
- [Matematica Financeira] Questão desafio
por CARLOS POVOAS » Qua Jun 19, 2013 00:35
- 0 Respostas
- 1788 Exibições
- Última mensagem por CARLOS POVOAS

Qua Jun 19, 2013 00:35
Matemática Financeira
-
- MATEMÁTICA FINANCEIRA - Equivalência financeira
 por ivolatanza » Ter Fev 28, 2017 15:33
por ivolatanza » Ter Fev 28, 2017 15:33
- 0 Respostas
- 10478 Exibições
- Última mensagem por ivolatanza

Ter Fev 28, 2017 15:33
Matemática Financeira
-
- Matemática Financeira
por plugpc » Sáb Jun 13, 2009 16:58
- 0 Respostas
- 9313 Exibições
- Última mensagem por plugpc

Sáb Jun 13, 2009 16:58
Vestibulares
-
- matematica financeira
por Joziani » Qui Abr 22, 2010 23:18
- 1 Respostas
- 6347 Exibições
- Última mensagem por Molina

Sex Abr 23, 2010 00:07
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


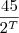 . Por outro lado, a cada período T o valor da lâmpada incandescente será
. Por outro lado, a cada período T o valor da lâmpada incandescente será  . Desejamos descobrir para que período t esses valores serão iguais. Temos então que:
. Desejamos descobrir para que período t esses valores serão iguais. Temos então que: