Considere as equações:
I. log(x + y) = log x + log y
II. x + y = xy
a) As equações I e II têm as mesmas soluções? Justifique.
Não necessariamente.
Caso x > 0 e y > 0 forem soluções da equação x + y = xy, então podemos aplicar o logaritmo em ambos os membros dessa equação, obtendo log(x + y) = log(xy) = log x + log y. Portanto, x e y também são soluções dessa última equação.
Por outro lado, caso x < 0 e y > 0 (ou ainda x > 0 e y < 0) forem soluções da equação x + y = xy, então não podemos aplicar o logaritmo em ambos os membros da equação, pois apareceria o logaritmo de um número negativo.
b) Esboce o gráfico da curva formada pelas soluções de I.
Você começou a solução, porém não soube terminar.
Utilizando as propriedades de logaritmos, desenvolvemos a equação I até obter xy = x + y.
Isolando y nessa equação, ficamos com
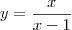
.
Note que para x e y serem positivos, basta escolher qualquer número x tal que x > 1. Portanto, o gráfico da função y = f(x) começa a partir de x > 1. Além disso, perceba duas coisas:
(i) se escolhemos x próximo de 1 (por exemplo, 1,1, 1,01, 1,001, 1,0001, etc) o valor de y é bem grande.
(ii) o valor de y é sempre maior do que 1, pois para calcular y nós estamos dividindo o número x pelo número x - 1, com isso temos uma fração cujo o numerador é sempre maior do que o denominador.
Agora, considerando essas informações e escolhendo alguns valores para x (por exemplo, 1,1, 1,2, 2, 3 e 4) você traçaria o esboço do gráfico abaixo.
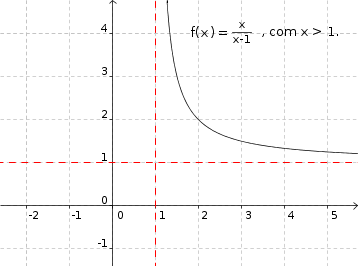
- gráfico.png (7.69 KiB) Exibido 2355 vezes
Vale lembrar que as linhas pontilhadas em vermelho são apenas para você se guiar.



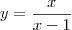 .
.
 Muito obrigado a todos que responderam, viu?
Muito obrigado a todos que responderam, viu?![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)