santiago alves escreveu: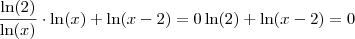
Imagine que você tenha um número n diferente de zero. Quanto vale a fração

? Ora, isso vale 1! Desse modo, o correto seria escrever:

Tome cuidado com as simplificações!
Agora, você tem a equação:

Para resolvê-la eu vou dar uma dica. Lembre-se da propriedade de logaritmos que diz que:
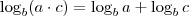
Aproveito também para lhe dar mais duas dicas:
- Para fazer uma revisão dos conteúdos do ensino fundamental ou médio, um bom lugar para começar é o canal do Nerckie no YouTube:
http://www.youtube.com/nerckie
- Se você desejar assistir um curso no YouTube sobre Cálculo Diferencial e Integral I, então eu espero que o meu canal possa ajudar:
http://www.youtube.com/LCMAquino
Observaçãosantiago alves escreveu:Livro: Matematica basica para ensino Superior. LOGARITMOS
Olá galera...
Estou estudando por este livro na esperaça de conseguir acompanhar o curso de calculo...
Bem, esse é um livro muito básico para um aluno do curso de engenharia. Procure não passar muito tempo utilizando ele como referência. É recomendado que você use um livro como, por exemplo, Cálculo Vol. 1 de James Stewart.




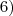
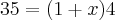
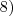
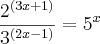


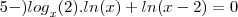

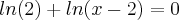
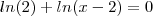
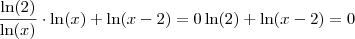
 ? Ora, isso vale 1! Desse modo, o correto seria escrever:
? Ora, isso vale 1! Desse modo, o correto seria escrever: