O valor real a e o menor entre os valores de x que satisfazem a equação
![2{log}_{2}(1+\sqrt[2]{2x})-{log}_{2}(\sqrt[2]{2x})=3 2{log}_{2}(1+\sqrt[2]{2x})-{log}_{2}(\sqrt[2]{2x})=3](/latexrender/pictures/f0626009da5a28929dc47587076ba7b8.png) .Então,
.Então,  é igual a:
é igual a:a)1/4
b)1/2
c)1
d)3/2
e)2
Agradeço desde ja

![2{log}_{2}(1+\sqrt[2]{2x})-{log}_{2}(\sqrt[2]{2x})=3 2{log}_{2}(1+\sqrt[2]{2x})-{log}_{2}(\sqrt[2]{2x})=3](/latexrender/pictures/f0626009da5a28929dc47587076ba7b8.png) .Então,
.Então,  é igual a:
é igual a:
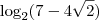 , que dá aproximadamente 0,425...
, que dá aproximadamente 0,425...



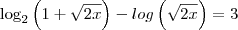
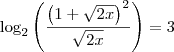


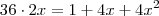

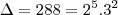 , nos dando uma raíz
, nos dando uma raíz  ...
...



Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.