 por vinicius cruz » Dom Mar 06, 2011 19:28
por vinicius cruz » Dom Mar 06, 2011 19:28
olá !!
será que alguem me explica como resolve essas equações ??
não sei como colocar a base do log no LATEX
a)log(12-2^x)(base2)=2x
B)logX(base3)=1+log9(baseX)
c)log(x+1)+1=log(x^2+35)
resp: a) log3(base2) b) 9 e 1/3 c) 5
-
vinicius cruz
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Dom Mar 06, 2011 12:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia civil
- Andamento: cursando
 por LuizAquino » Dom Mar 06, 2011 19:40
por LuizAquino » Dom Mar 06, 2011 19:40
vinicius cruz escreveu:não sei como colocar a base do log no LATEX
Use o comando:
- Código: Selecionar todos
[tex]\log_2 x[/tex]
O resultado é:

Farei um dos exercícios e você tenta fazer os outros.
a)

Aplicando a definição do logaritmo:

Fazendo a substituição

, obtemos a equação:
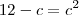
A solução dessa equação é
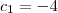
ou

.
Sendo assim temos que
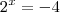
ou

.
A primeira dessas equações não tem solução. Já a segunda tem solução

.
b)
 Sugestão
SugestãoUse mudança de base para transformar o logaritmo com base x em um novo logaritmo com base 3.
Além disso, lembre-se que

e que
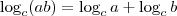
.
c)
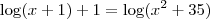 Sugestão
SugestãoLembre-se que
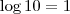
e que
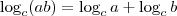
.
Editado pela última vez por
LuizAquino em Dom Mar 06, 2011 19:45, em um total de 2 vezes.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por vinicius cruz » Dom Mar 06, 2011 19:42
por vinicius cruz » Dom Mar 06, 2011 19:42
como colocou a base do log no latex ?
-
vinicius cruz
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Dom Mar 06, 2011 12:47
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia civil
- Andamento: cursando
 por LuizAquino » Dom Mar 06, 2011 19:54
por LuizAquino » Dom Mar 06, 2011 19:54
vinicius cruz escreveu:como colocou a base do log no latex ?
Veja o que escrevi antes:
LuizAquino escreveu:Use o comando:
- Código: Selecionar todos
[tex]\log_2 x[/tex]
O resultado é:

O "\log" é para a função logarítmica. O "_" (sublinhado) é para colocar símbolos em subscrito.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equações Logarítmicas
por Danilo Dias Vilela » Qua Set 01, 2010 11:21
- 1 Respostas
- 1589 Exibições
- Última mensagem por MarceloFantini

Qua Set 01, 2010 21:56
Álgebra Elementar
-
- equações logarítmicas
por Luan Cordeiro » Qui Ago 04, 2011 20:42
- 2 Respostas
- 1962 Exibições
- Última mensagem por Claudin

Sex Ago 05, 2011 01:34
Logaritmos
-
- equações logarítmicas
por Luan Cordeiro » Sáb Ago 06, 2011 19:20
- 1 Respostas
- 1499 Exibições
- Última mensagem por LuizAquino

Dom Ago 07, 2011 13:39
Logaritmos
-
- Equações Logarítmicas
 por lucassouza » Qua Nov 05, 2014 17:35
por lucassouza » Qua Nov 05, 2014 17:35
- 1 Respostas
- 1549 Exibições
- Última mensagem por Russman

Qua Nov 05, 2014 23:05
Logaritmos
-
- Equações Logarítmicas (cont)
 por lucassouza » Qui Nov 06, 2014 00:28
por lucassouza » Qui Nov 06, 2014 00:28
- 2 Respostas
- 1811 Exibições
- Última mensagem por lucassouza

Qui Nov 06, 2014 15:59
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.






 , obtemos a equação:
, obtemos a equação: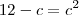
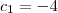 ou
ou  .
.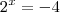 ou
ou  .
. .
.
 e que
e que 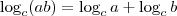 .
.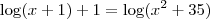
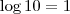 e que
e que 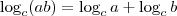 .
.


