Em algumas regiões do Brasil, as tomas elétricas padrão fornecem uma corrente elétrica senoidal com uma voltagem máxima de V= 120raizde2 volts(v), a uma frequência de 60 ciclos por segundo.
então os dados que tenho é V= 120raisde2 e a frequência 60s e pede para escrever a equação que expressa V como função do tempo dai diz que V=0 em T=0
que equação eu posso utilizar para resolver esse exercício? Quero muito saber resolver esta questão. Muito Obrigado
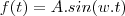
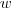de frequência angular e é possível mostrar que 
é o valor máximo dessa função.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
o ângulo entre o eixo horizontal e o afixo 
. O triângulo é retângulo com catetos 
e 
, tal que 
. Seja 
o ângulo complementar. Então 
. Como 
, o ângulo que o afixo 
formará com a horizontal será 
, então 
. Como módulo é um: 
.
.